实验条件
-
环境:多臂老虎机
-
臂数 (K): 10
-
步数 (T): 10^5
-
每个臂的的奖励分布:X\sim\text{Bernoulli}(\theta_i)\\ \text{其中,}\theta_i=\frac{i}{K+1}\ ,(i\in\{1,2,3...,K\})
-
算法:Greedy
-
表达式:a_{t+1} = \arg\max_{a\in \{1,2,3,...,A\}}\hat{Q}_t(a)\\ \text{其中,}\hat{Q}_t(a)= \begin{cases} Q_0 &\text{如果动作 a 还没有被选择过}\\ \frac{1}{N_t(a)}\sum_{i:A_i=a}^{t}R_i & \text{如果动作 a 已经被选择过} \end{cases}
-
Q_0 = 1
-
参数:
- \hat{Q}_t(a)\text{: 对动作 a 在 t 时刻的回报真实值估量}
- N_t(a)\text{: 到时刻 t 为止,动作 a 的执行次数}
- A\text{: 动作空间}
- R_i\text{: i 时刻的奖励}
- Q_0\text{: 乐观初始化值}
-
-
算法:UCB1
-
表达式:a_{t+1}=\arg\max_{a\in{\{1, 2, 3, ..., A\}}}\left[\ \hat{Q}_t(a)+\sqrt{\frac{2\ln{t}}{N_t(a)}}\ \right]\\ \text{其中,}\hat{Q}_t(a)=\frac{1}{N_t(a)}\sum_{i:A_i=a}^{t}R_i
-
参数:
- \hat{Q}_t(a)\text{: 对动作 a 在 t 时刻的回报真实值估量}
- N_t(a)\text{: 到时刻 t 为止,动作 a 的执行次数}
- A\text{动作空间}
- R_i\text{: i 时刻的奖励}
-
-
算法:Thompson\ Sampling
-
表达式:a_{t+1}=\arg\max_{a\in\{1,2,3,...,A\}}\tilde{Q}_t(a)\\ \text{其中,} \tilde{Q}_t(a)\sim\text{Beta}\left(S_t(a)+1, F_t(a)+1\right)
参数:
- \tilde{Q}_t(a)\text{: 对于动作 a 从 Beta 后验分布中采样得到的动作价值}
- S_t(a)\text{: 到时刻 t 为止动作 a 获得成功的次数}
- F_t(a)\text{: 到时刻 t 为止动作 a 获得失败的次数}
-
-
重复运行次数(R):500
- 说明:同一次重复运行中,每个 Agent 的种子均不同,不同重复运行的 Agent 种子均相同。所有重复运行的环境种子均相同。
-
实验目的:比较不同步数下 UCB1 和贪心算法的性能
-
对比不同的K下:
- 累积奖励的曲线如何随时间的变化
- 累积的后悔值曲线
- 后悔率曲线
- 最佳臂命中率曲线
- 收敛率
- 收敛速度(多少步达到收敛)
-
-
收敛:最佳臂命中率达到 90% 及以上时,可以认为是收敛
实验记录
指标对比
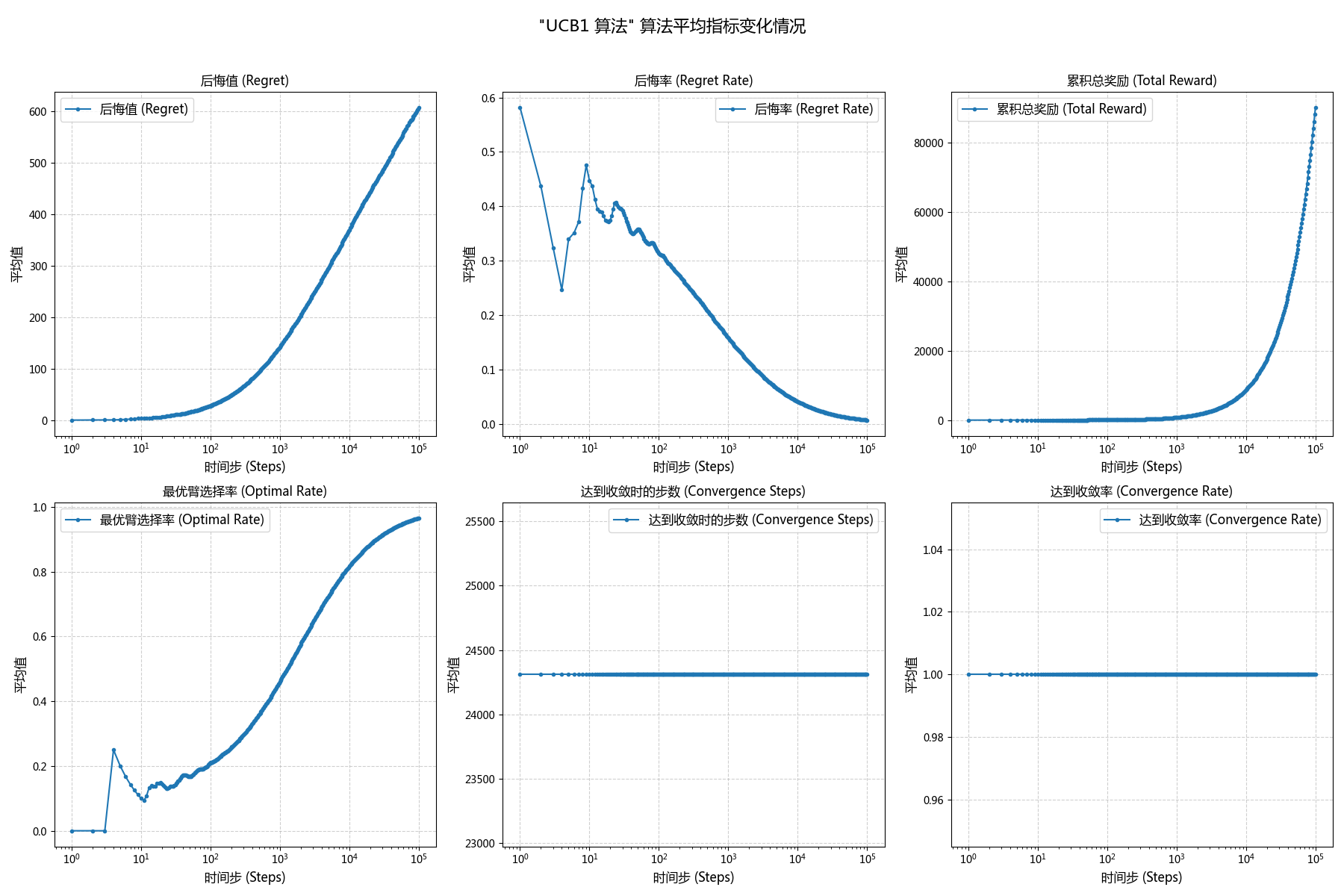
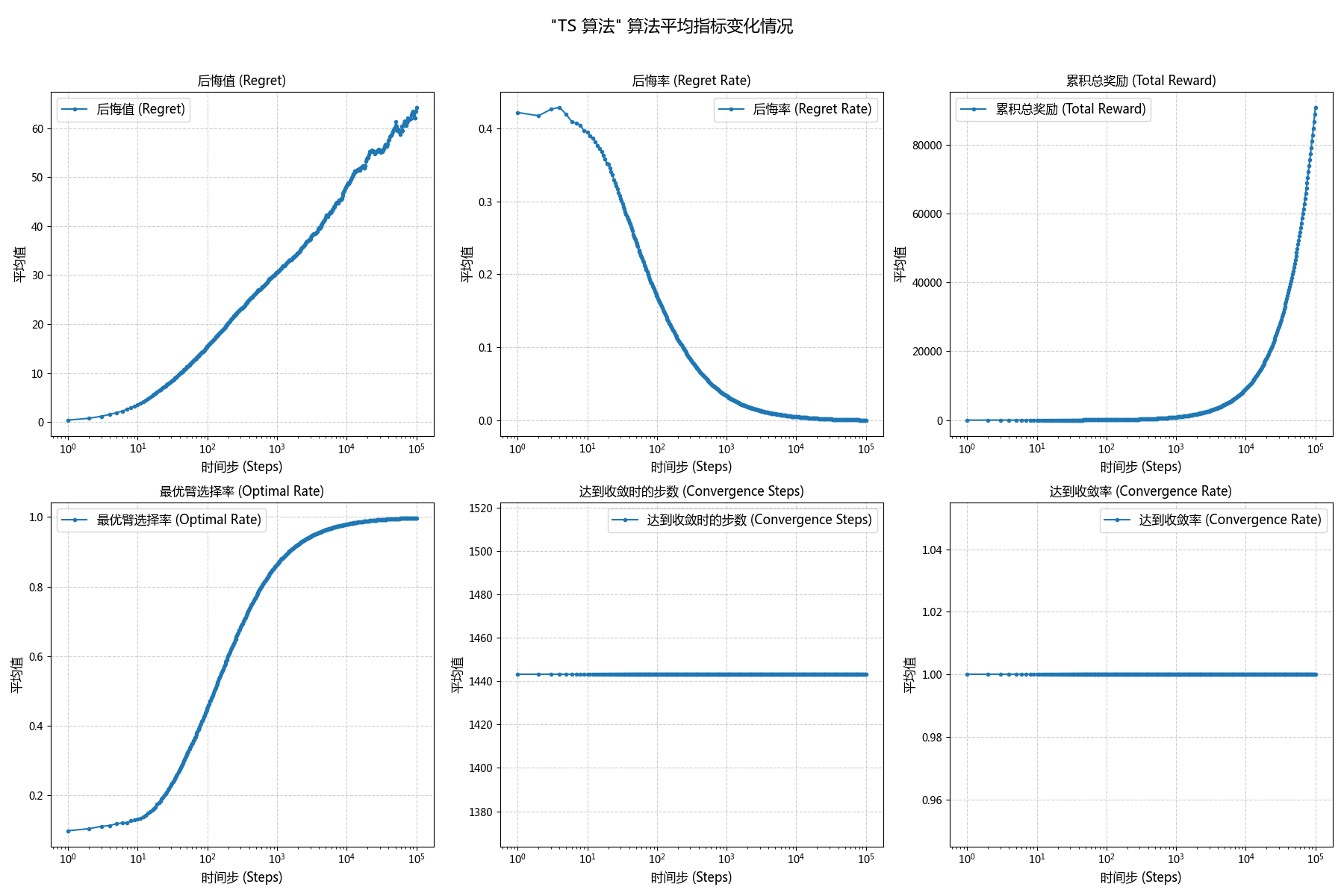
| 算法名称 | 遗憾值 | 遗憾率 | 累积奖励 | 最优动作率 | 收敛步数 | 收敛率 |
|---|---|---|---|---|---|---|
| Greedy | 3660.13 | 0.0403 | 87248.96 | 0.7178 | 245.88 | 0.718 |
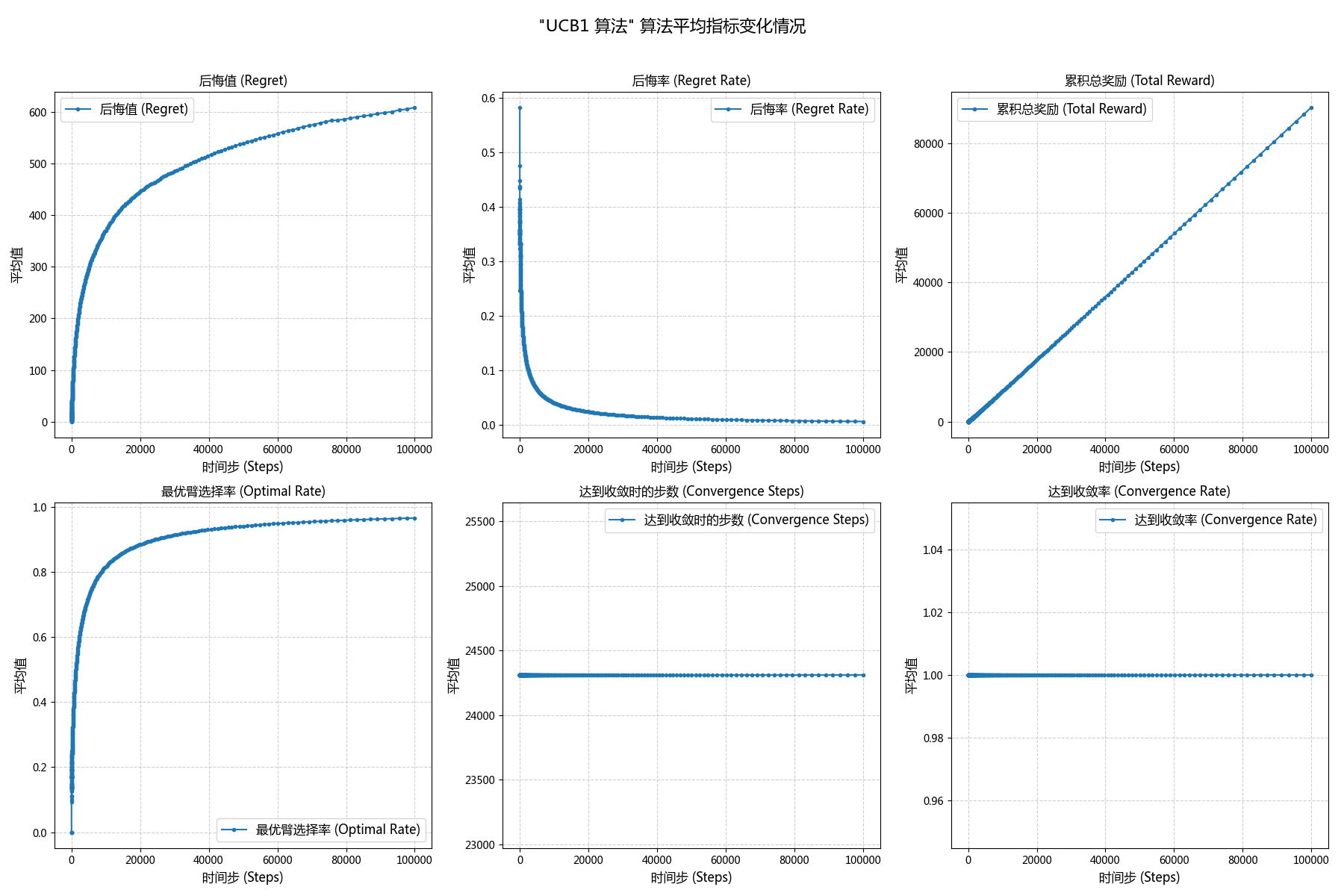
| UCB1 | 608.33 | 0.0067 | 90300.76 | 0.9662 | 24310.90 | 1.00 |
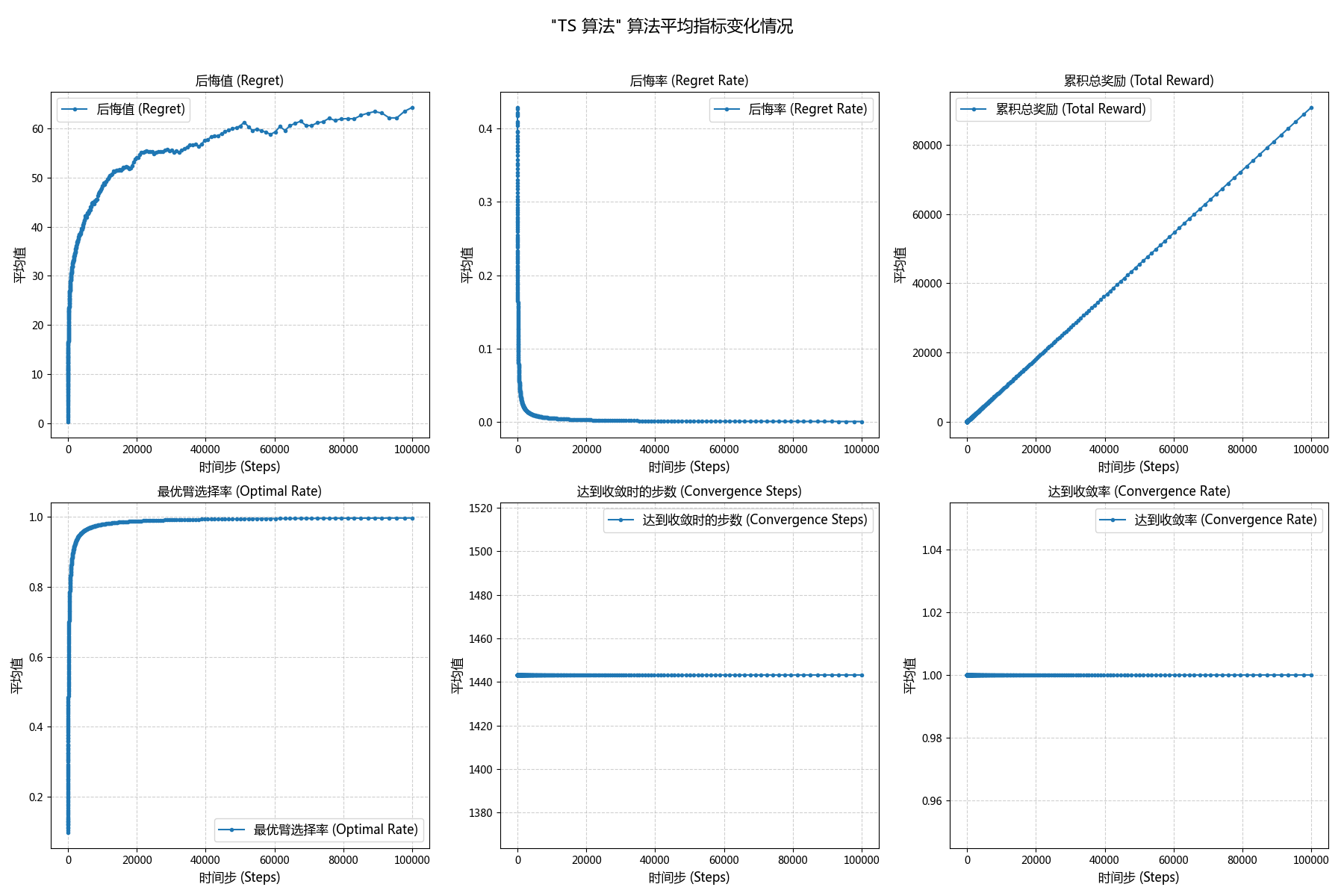
| Thompson\ Sampling | 64.24 | 0.0007 | 90844.85 | 0.9971 | 1443.18 | 1.00 |
过程数据图表
| X 轴增长方式 | Greedy | UCB1 | Thompson\ Sampling |
|---|---|---|---|
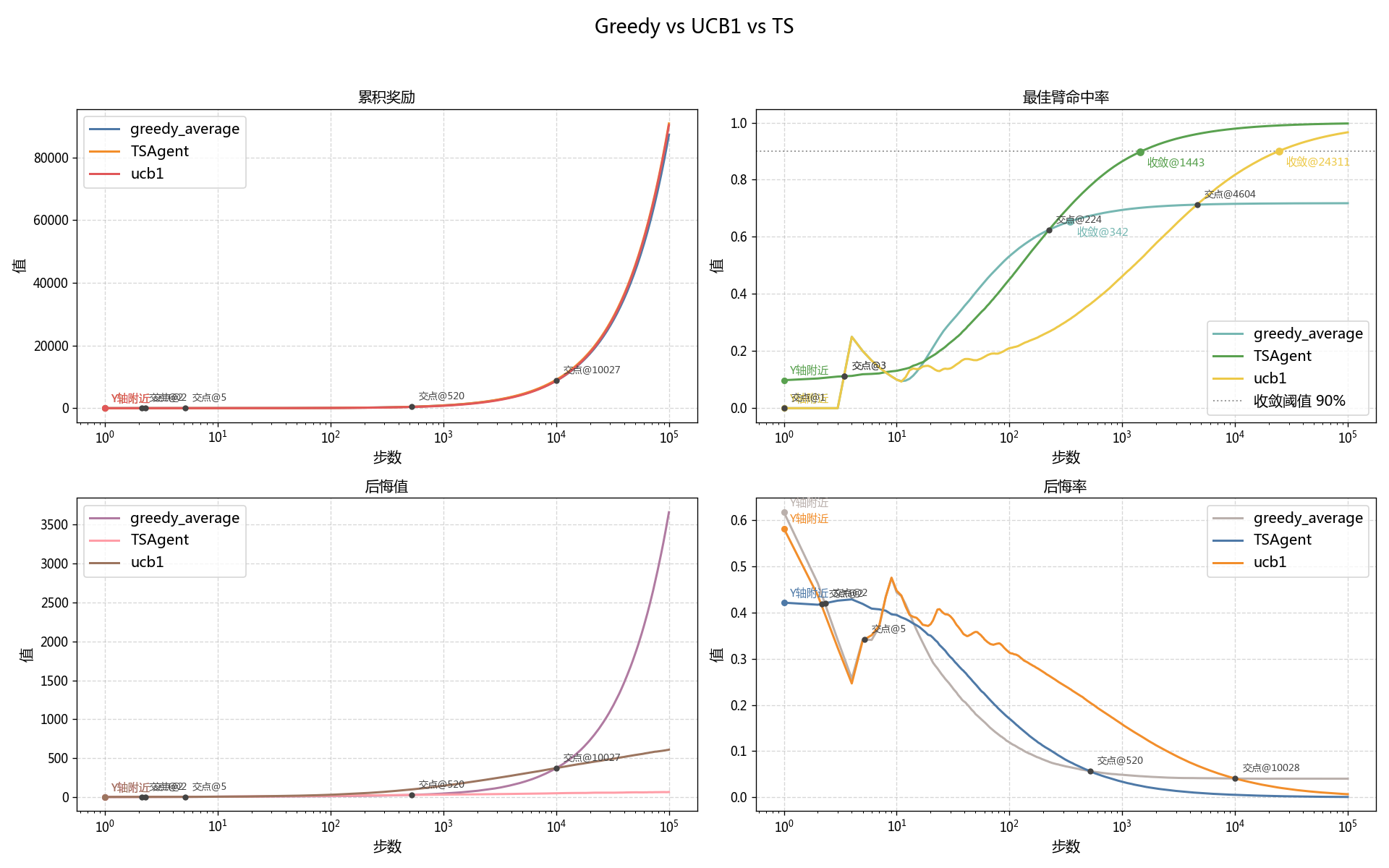
| 线性增长 | 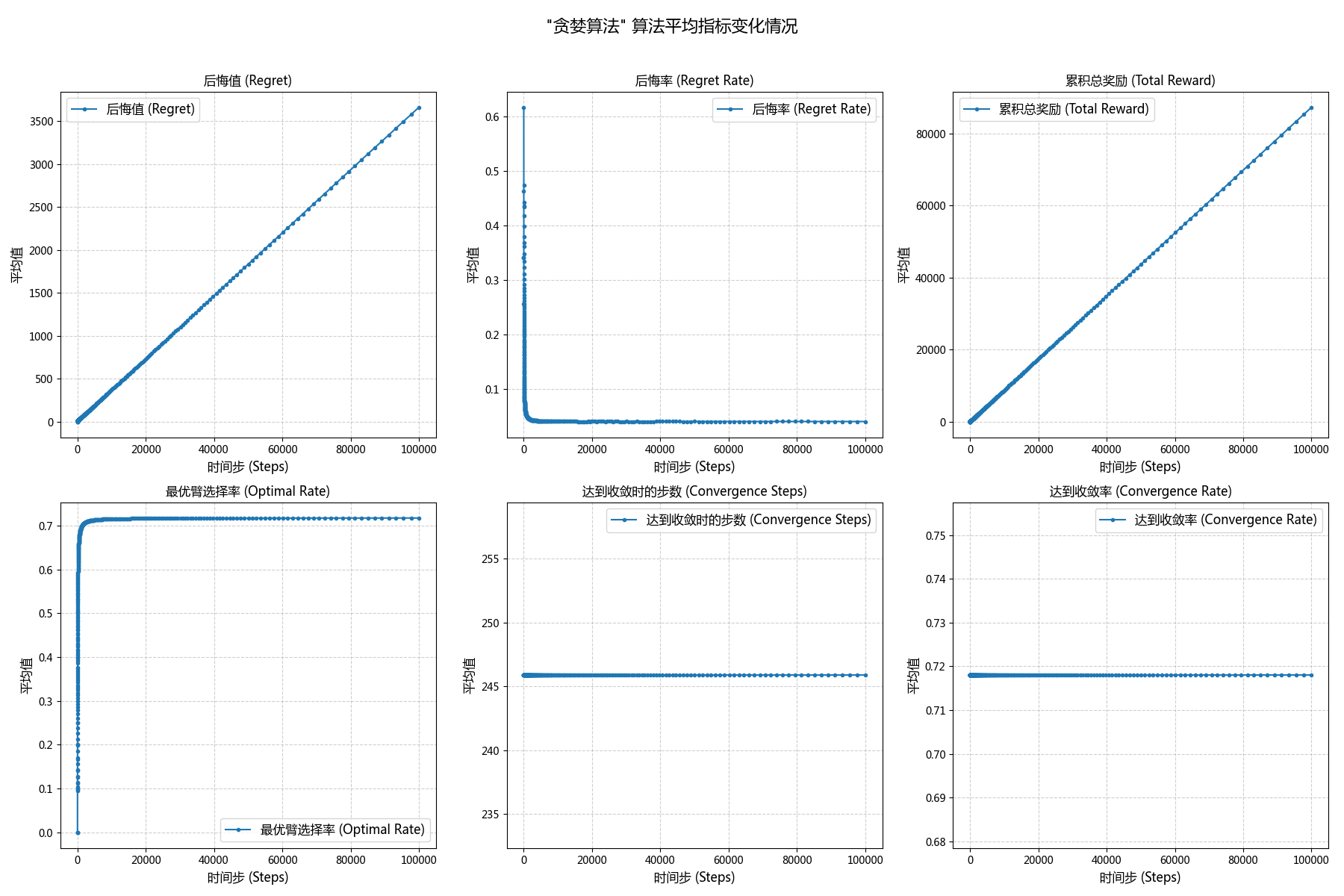 |
 |
 |
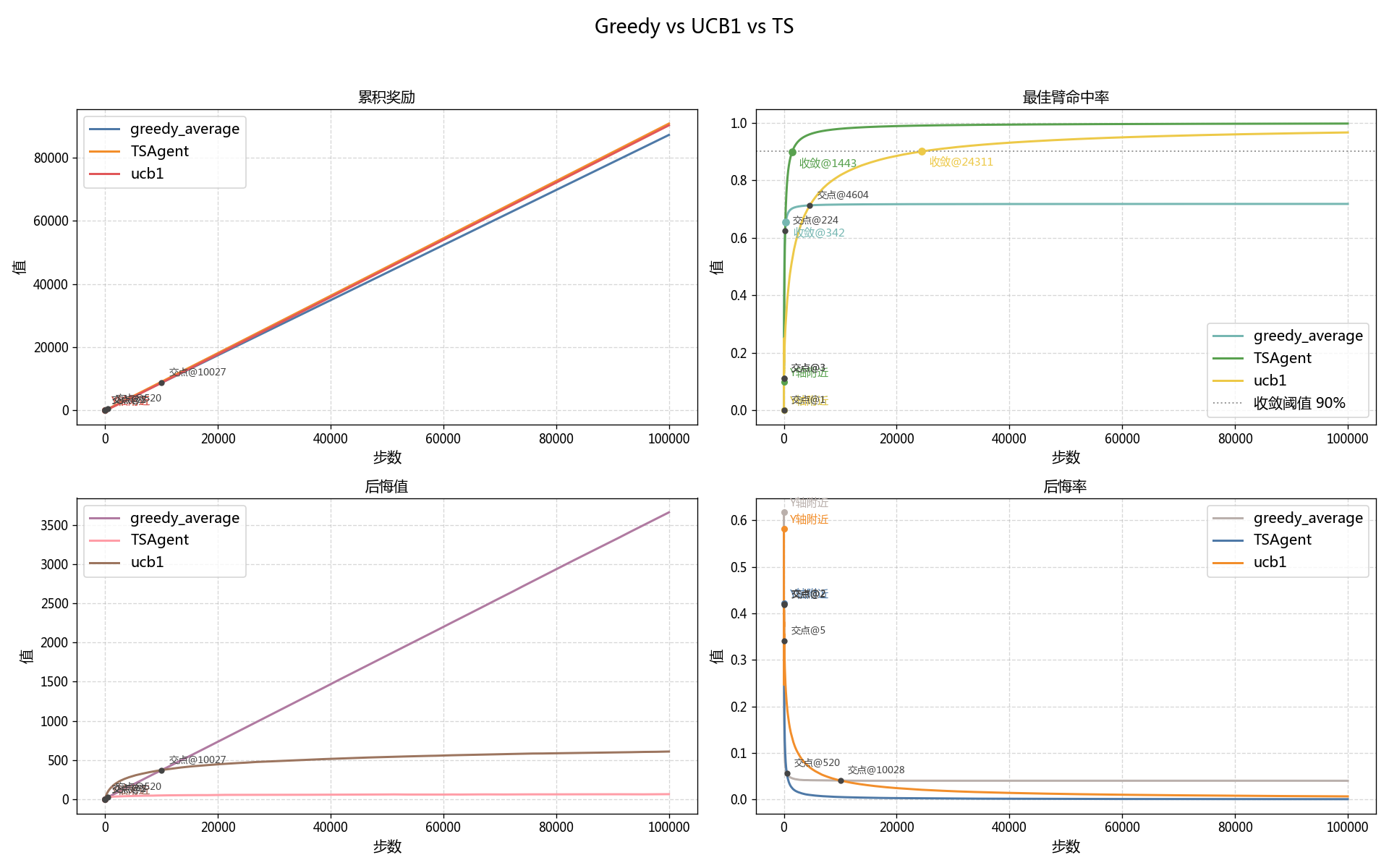
| 指数增长 | 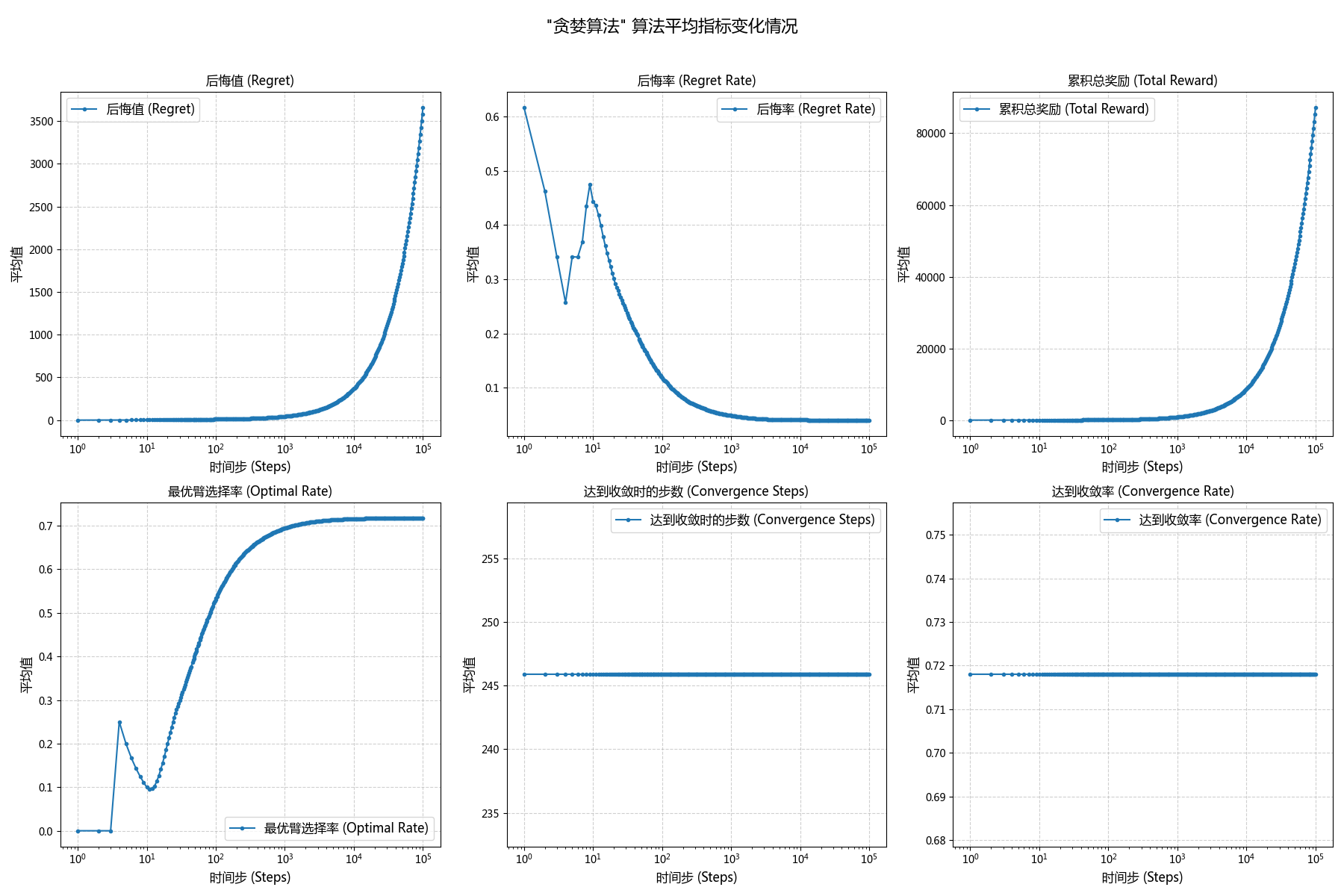 |
 |
 |
过程数据图表 (Greedy vs UCB1 vs TS)
| X-线性增长 | X-指数增长 |
|---|---|
 |
 |
实验现象
-
初版:
-
对于累积奖励:三者的累积奖励在早期的差距并不大,但是在 $t>10027$ 后,UCB1 和 TS 的累积奖励逐渐优于贪婪算法,并在 $t\approx5*10^4$ 时明显优于贪婪算法。但是二者后续差距并不大。
-
而对于最佳臂命中率,大约$20 <t<224$时,贪婪算法的命中率略优于 TS,而在 $t>224$后,贪婪算法的最优臂命中率则被 TS 远远超过。
类似的,在大约$20<t<4604$时,贪婪算法的最优臂命中率大幅优于 UCB1,而在 $t>4604$后,贪婪算法的最优臂命中率则被 UCB1 远远超过。
-
除此之外,贪婪算法的收敛率只有 0.7178,而 UCB1 和 TS 都达到了绝对收敛,两者分别是在 $t=24311$ 与 $t=1443$ 时达到收敛的。
为了比较在 $T=10^5$ 时各算法收敛率的差异显著性,我们进行Z检验统计量计算:
- TS vs UCB1: z_{TS-UCB1} = 3.6403, \quad p_{TS-UCB1} = 0.0003 < 0.01
- UCB1 vs Greedy: z_{UCB1-Greedy} = 10.7680, \quad p_{UCB1-Greedy} < 0.0001
结果表明:
\boxed{r_{TS} \triangleright r_{UCB1} \triangleright r_{Greedy}}- 对于后悔值,贪婪则呈线性趋势,一直保持一定的斜率;UCB1 和 TS 均则成对数趋势,一开始斜率较高,后续则近似于 0。
- 对于后悔率,贪婪在 t<520 前均持续下降,但是在 t\ge520 后斜率也趋近于0;而 UCB1 和 TS 相比,后者的下降速度快于前者,并且两者数值上均最终无限接近于0 。
-
-
修订版:
通过对三种算法在10^5内的各项指标进行观察和对比,我们发现了以下实验现象:
- 总体性能:Thompson Sampling 表现最优,Greedy 陷入局部最优。
从最终的累计奖励、累积后悔值和最佳臂命中率等多个核心指标来看,三种算法的综合性能排序为:Thompson\ Sampling\triangleright{UCB1}\triangleright{Greedy}。
Thompson Sampling(TS) 算法在收敛速度和最终效果上均表现最佳。UCB1 算法虽然也能收敛到最优解,但其探索过程更为漫长。而 Greedy 算法由于其策略的局限性,在早期做出次优的决定后便陷入了局部最优,无法达到理想的性能。
- 最佳臂命中率与收敛性分析
最佳臂命中率是衡量算法能否准确找到并持续选择最优动作的关键指标。
-
早期阶段(t<500):从过程数据图表(Greedy vs UCB1 vs TS)的 X-指数增长的这张图中可以清晰的看到,在最初的几十步中,Greedy 凭借其乐观初始化(Q_0=1)的早期优势,迅速锁定的目前看起来最优的臂,因此其命中率早期(约t\in{\left[20, 4604\right]})领先于正在进行广泛探索的 UCB1 算法和 TS 算法。
-
中期探索与超越:随着步数的增加,UCB1 和 TS 算法通过持续的探索,逐渐获得了对所有臂更准确的价值估计。
- 在t\approx224步以后,TS 算法的命中率超越了 Greedy 算法。
- 而 UCB1 的探索则更为保守和漫长,直到t\approx4604步后,其命中才完成对 Greedy 算法的超越。
-
后期收敛状态:在试验后期(t\rightarrow10^5)
- Greedy 的命中率收敛于约 71.8% ,表明其已陷入局部最优,无法稳定选择真正奖励最高的臂。
- UCB1 和 TS 算法都表现出了优秀的收敛性,命中率均趋近于 100% 。TS 算法在 t\approx1443 步时命中率就达到了 90% 的收敛标准,而 UCB1 则需要约 t\approx24311,显示出 TS 在收敛速度上远优于 UCB1。
为了验证最终收敛率的差异是否显著,我们进行了 Z 检验,结果显示:
- TS vs UCB1: z=3.64, p<0.01
- UCB1 vs Greedy: z=10.77, p<0.001
这在统计学上证明了三种算法在最终最佳臂选择能力上存在显著差异,与我们的观感相符:
\boxed{r_{TS}\triangleright{r_{UCB1}}\triangleright{r_{Greedy}}}- 累积奖励分析
累积奖励直观地反映了算法在整个过程中的收益。
- 曲线整体上,三种算法的累积奖励都随步数增加而近似线性增长。但是,增长的斜率代表了算法在稳定状态下选择臂的平均奖励。
- 在t>10027步之后,UCB1 和 TS 算法的累积奖励曲线斜率明显高于 Greedy 算法,并最终与之拉开显著差异。
- TS 和 UCB1 在实验后期累积奖励值非常接近,但 TS 凭借更快的收敛速度,在整个生命周期内获得了略高的总奖励(90844.85 vs 90300.76)
- 累积后悔值和后悔率分析
后悔值是衡量探索与利用代价的关键指标。
-
累积后悔值:
- Greedy 算法的累积后悔值呈现出线性增长的趋势,这正是陷入局部最优的直接体现——在每个时间步,几乎都是在犯同样的“错误”,从而累积了线性增长的遗憾。
- 相比之下,UCB1 和 TS 算法则呈现出对数增长的趋势。曲线在早期斜率较大(探索代价),后期则趋于平缓,表明算法收敛后产生的后悔值极低。
-
后悔率:
- 所有算法的后悔率在一开始都迅速下降。
- Greedy 的后悔率在t\approx520后趋于一个非零的常数(约0.04),这意味着它平均每一步都会损失固定的奖励。
- UCB1 和 TS 的后悔率则持续下降并无限趋近于 0,表明它们最终能做到几乎“不再后悔”。其中,TS 的后悔率下降速度显著快于 UCB1。
实验结论
-
初版:
这三种算法中,总体性能最好的是 TS 算法,Greedy 和 UCB1 各有优劣。
UCB1 在早期t<10^3由于持续探索,表现普遍不如 Greedy 算法;然而在长时间尺度(t>10^4)下,它能够逐步反超,并最终实现对最优臂的稳定收敛。
相比之下,Greedy 虽然在早期就可以快速累积奖励、降低后悔率和快速命中最优臂,但是常常陷入局部最优导致后期只能持续命中次优臂,无法收敛。
TS 算法虽然早期性能表现通常不如 Greedy 算法,但是在中期(t\in[1000, 2000])往往都可以获得超越 Greedy 的性能,且速度远快于 UCB1 算法。
这说明 TS 算法的性能相较于另外两者,确实在收敛性上有显著优势;Greedy 算法因为容易陷入局部最优,通常在前期表现最好,但是性能会在时间尺度的拉长下被 TS 算法快速超过,在更长的时间尺度下会被 UCB1 算法超过;而 UCB1 算法则牺牲了前期和中期的大量探索才换来了后期稳定优秀的性能表现。
-
修订版:
本次实验系统地比较了 Greedy, UCB1, 和 Thompson Sampling (TS) 算法的在静态多臂老虎机问题上的性能。实验结论如下:
-
核心结论:Thompson Sampling 的综合性能最优,它在“探索与利用”的权衡中展现了最高的效率。 Greedy 算法因为无法进行有效的探索而陷入局部最优,而 UCB1 算法虽然能保证收敛,但其探索代价过高。
-
算法策略的权衡分析:
- Greedy (纯利用策略) :该算法验证了纯利用策略的内在缺陷。尽管其乐观初始化在实验极早期(约前 500 步)表现出优势,但一旦因随机性选择了次优臂,便缺乏纠错机制,导致其长期性能最差,累积后悔值呈线性增长。
- UCB1 (确定性探索策略): 该算法代表了一种稳健但保守的探索方式。它通过置信上界项强制对选择次数最少的臂进行探索,从而保证了渐进最优性, 最终能够收敛。然而,这种系统性的探索的效率并不高,导致在中后期(直到约10027步前)性能均落后于 Greedy ,是一种典型的“牺牲短期收益以换取长期保障”的策略。
- Thompson Sampling (概率性探索策略) :该算法通过对臂真实价值的后验分布进行采样,实现了一种更智能、更高效的探索。它根据不确定性的大小来自然地调整探索力度,因此能比 UCB1 更快地(约 1443 步达到 90%最佳臂命中率) 识别出最优臂,同时有效避免了 Greedy 的局部最优陷阱。
-
总结和启示: 实验结果明确表明,在静态 Bandit 问题中,算法对“不确定性”的建模和处理方式是决定其性能的关键。 Thompson Sampling 所代表的贝叶斯方法,能够高效地量化和利用不确定性信息指导决策,从而在整体性能上超越了纯贪心策略和基于确定性区间的策略。
-

