实验条件

• 环境：多臂老虎机（动态环境）

• 臂数 (​K): 10

• 步数 (​T): ​10^5

• 每个臂的的奖励分布：​X\sim\text{Bernoulli}(\theta_i)\\ \text{其中，}\theta_i=\frac{i}{K+1}\ ,(i\in\{1,2,3...,K\})

• 环境随机漫步表达式：​r_i^{(t+1)} = \begin{cases} r_i^{(t)} + \varepsilon_i & if \ 0 \leq r_i^{(t)}+\varepsilon_i\leq1 \\ r_i^{(t)} - \varepsilon_i & otherwise \end{cases}

  其中：

  • ​r_i^{(t)}表示在第 ​i 个机器在 ​t 时刻的奖励概率。
  • ​\epsilon_i\sim\mathcal{N}(0,0.01^2) 是从正态分布采样的随机扰动。
  • 随机漫步间隔：1
  • 每次随机漫步影响的机器数量：10

• 算法：​Greedy

  • 表达式：​a_{t+1} = \arg\max_{a\in \{1,2,3,...,A\}}\hat{Q}_t(a)\\ \text{其中，}\hat{Q}_t(a)= \begin{cases} Q_0 &\text{如果动作 a 还没有被选择过}\\ \hat{Q}_{t-1}(a)+\alpha\cdot(R_{t}-\hat{Q}_{t-1}(a)) & \text{如果动作 a 已经被选择过} \\ \hat{Q}_{t-1}(a) +\frac{1}{N_{t}(a)}\cdot(R_t-\hat{Q}_{t-1}(a)) & \text{Baseline Greedy} \end{cases}

  • ​Q_0 = 1

  • 参数：

    • ​\hat{Q}_t(a)\text{: 对动作 a 在 t 时刻的回报真实值估量}
    • ​\alpha:常数步长值（以下亦称“学习率”）
    • ​A\text{: 动作空间}
    • ​R_t\text{: t 时刻的奖励}
    • ​Q_0\text{: 乐观初始化值}

  • 基线：样本均值更新方式的 ​Greedy，带乐观初始化

• 重复运行次数(​R)：500

  • 说明：同一次重复运行中，每个 Agent 的种子均不同，不同重复运行的 Agent 种子均相同。所有重复运行的环境种子均相同。

• 实验中所设置的常数步长值：

  • 0.001
  • 0.005
  • 0.01
  • 0.05
  • 0.1
  • 0.3
  • 0.5
  • 0.7
  • 0.9
  • 0.99
  • 0.999
  • 0.9999
  • 0.99999

• 实验目的：比较不同 ​\alpha 下贪心算法的性能

• 指标

  • 后悔率（以“动态最优”为基准（即每步对比当时刻最优臂））
  • 后悔值（以“动态最优”为基准（即每步对比当时刻最优臂））
  • 奖励率
  • 奖励值
  • 最佳臂命中率（是否按每个 ​t 的瞬时最优臂统计）
  • 滑动窗口奖励率（滑动窗口大小为 1000，对齐方式为右对齐）

实验记录

聚合图表

• 指标散点图：

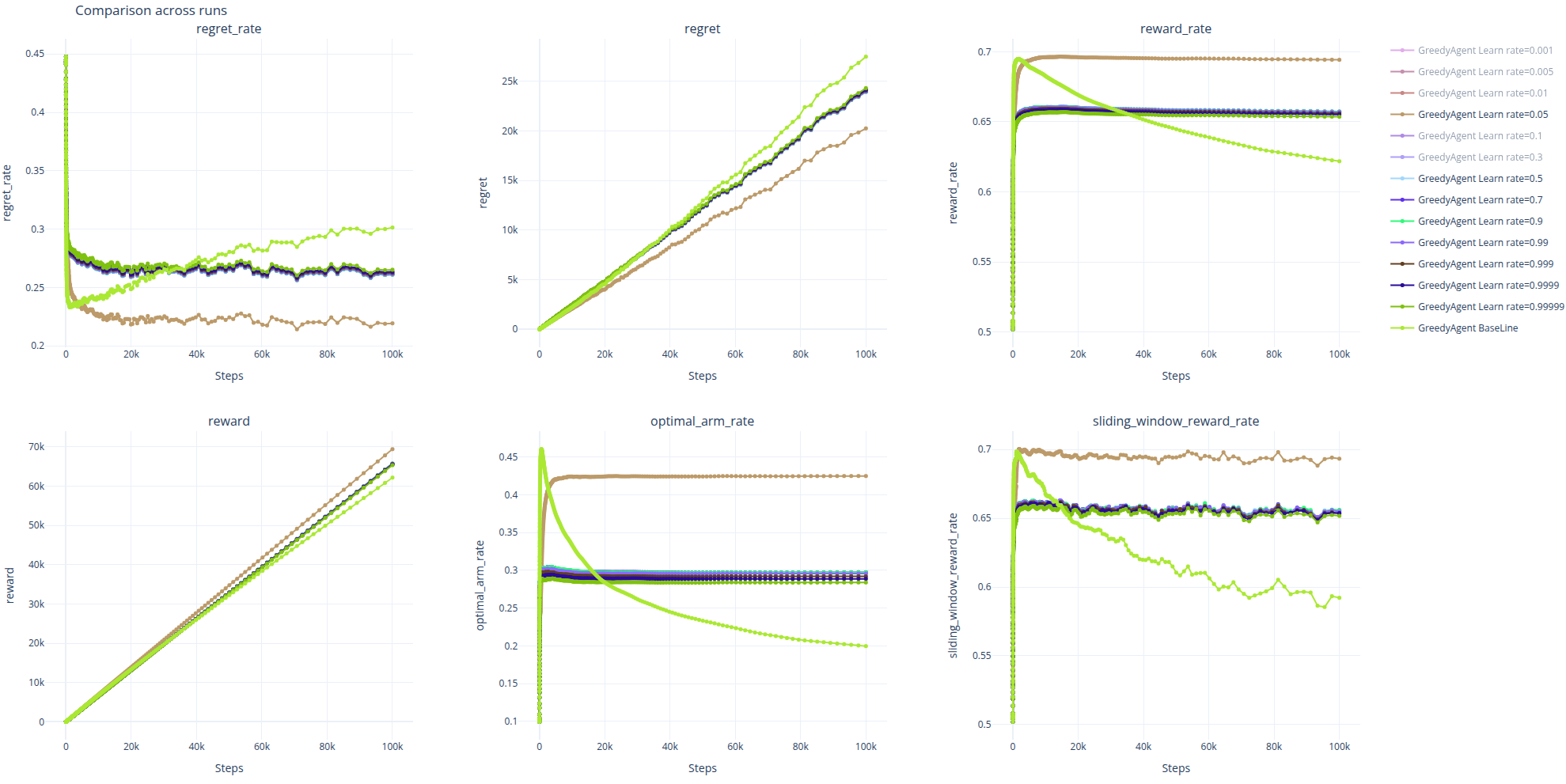
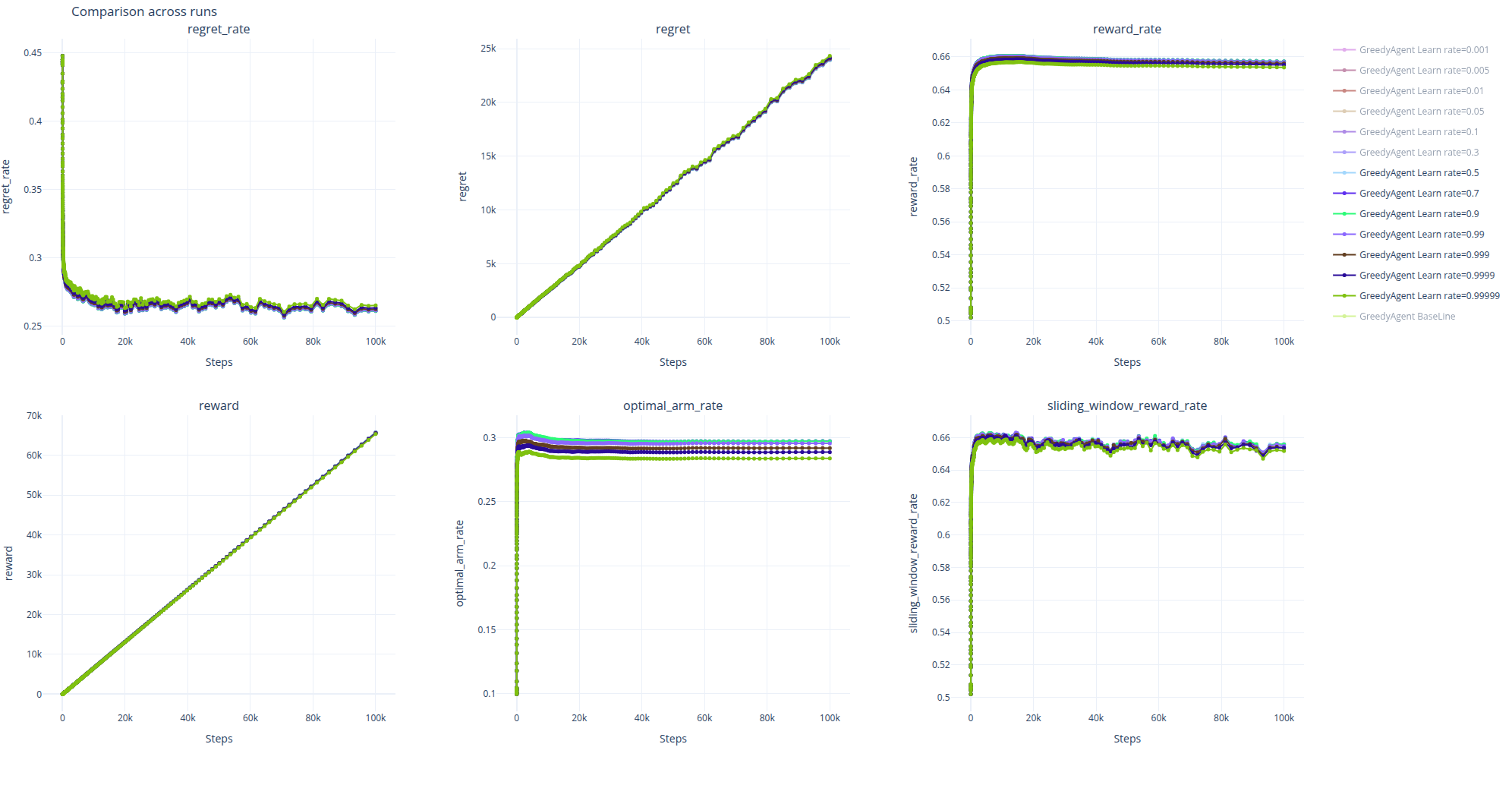
  下图展示了不同学习率下各性能指标随训练步数（横轴，对数尺度）的变化情况。图中的实线代表 500 次重复实验的均值，半透明的阴影区域代表 95% 置信区间 (95% CI) 。置信区间越窄，表明对该算法性能的估计越精确和稳定。

X-线性增长	X-指数增长

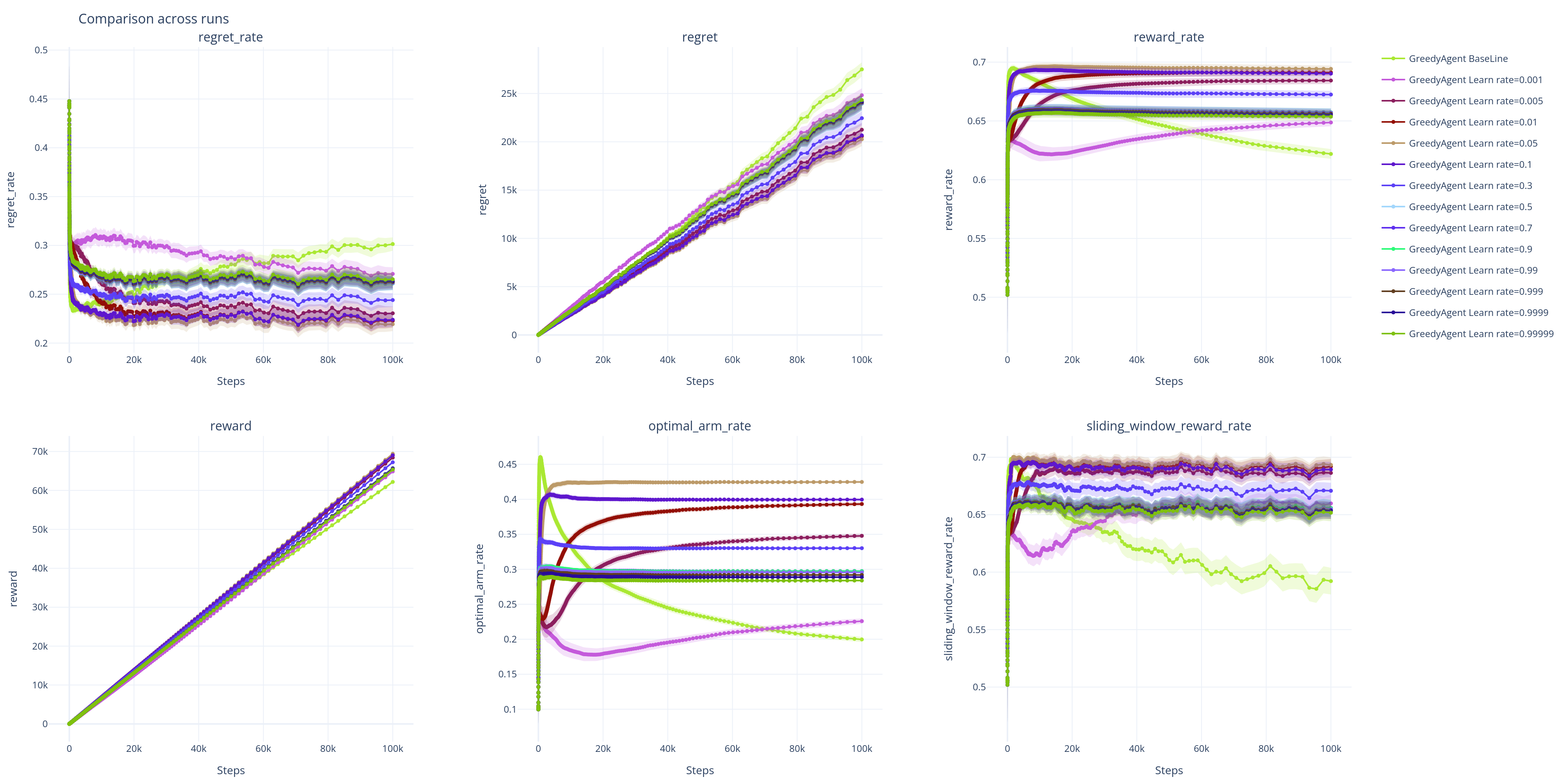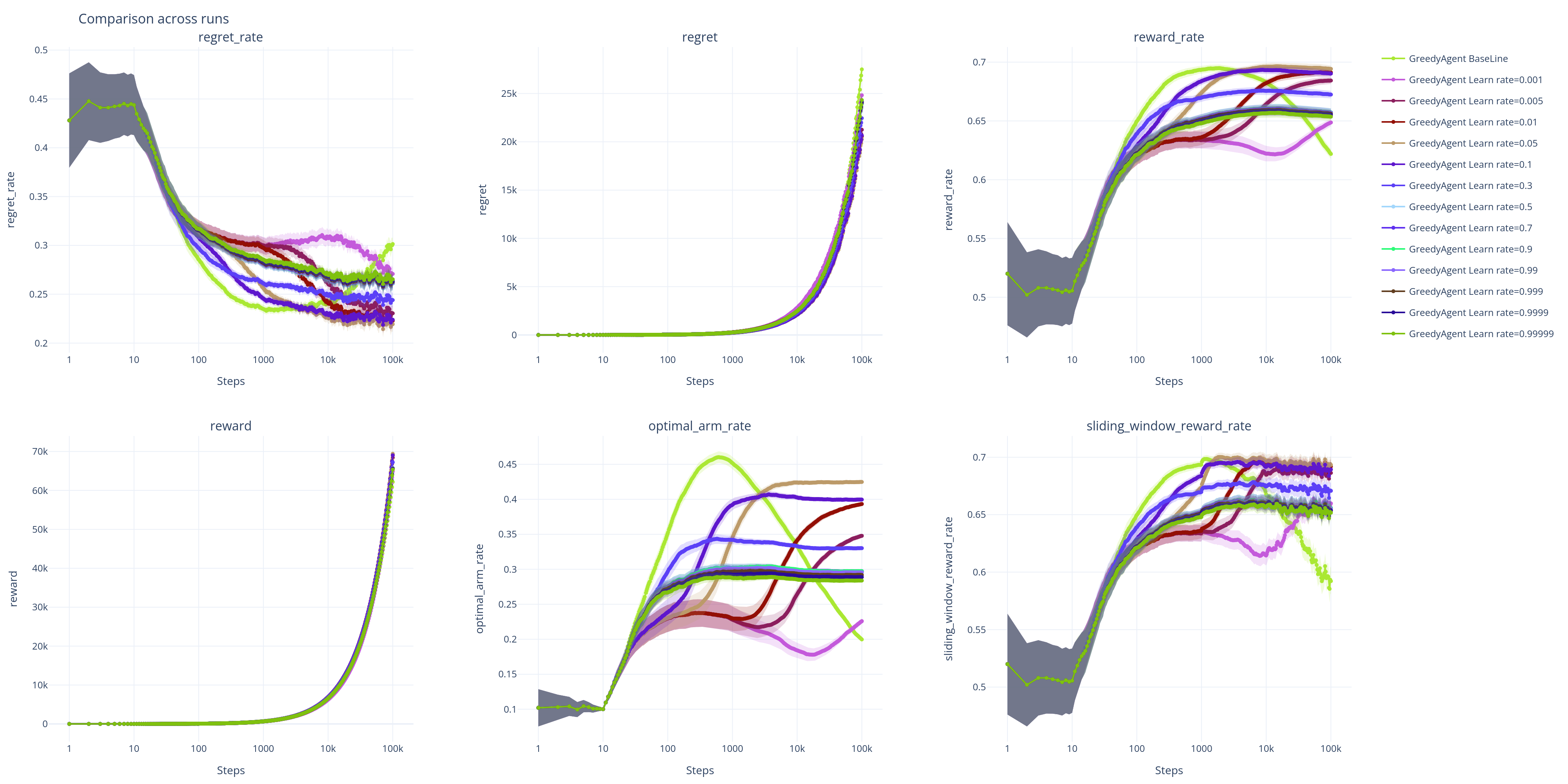• 指标表格

  

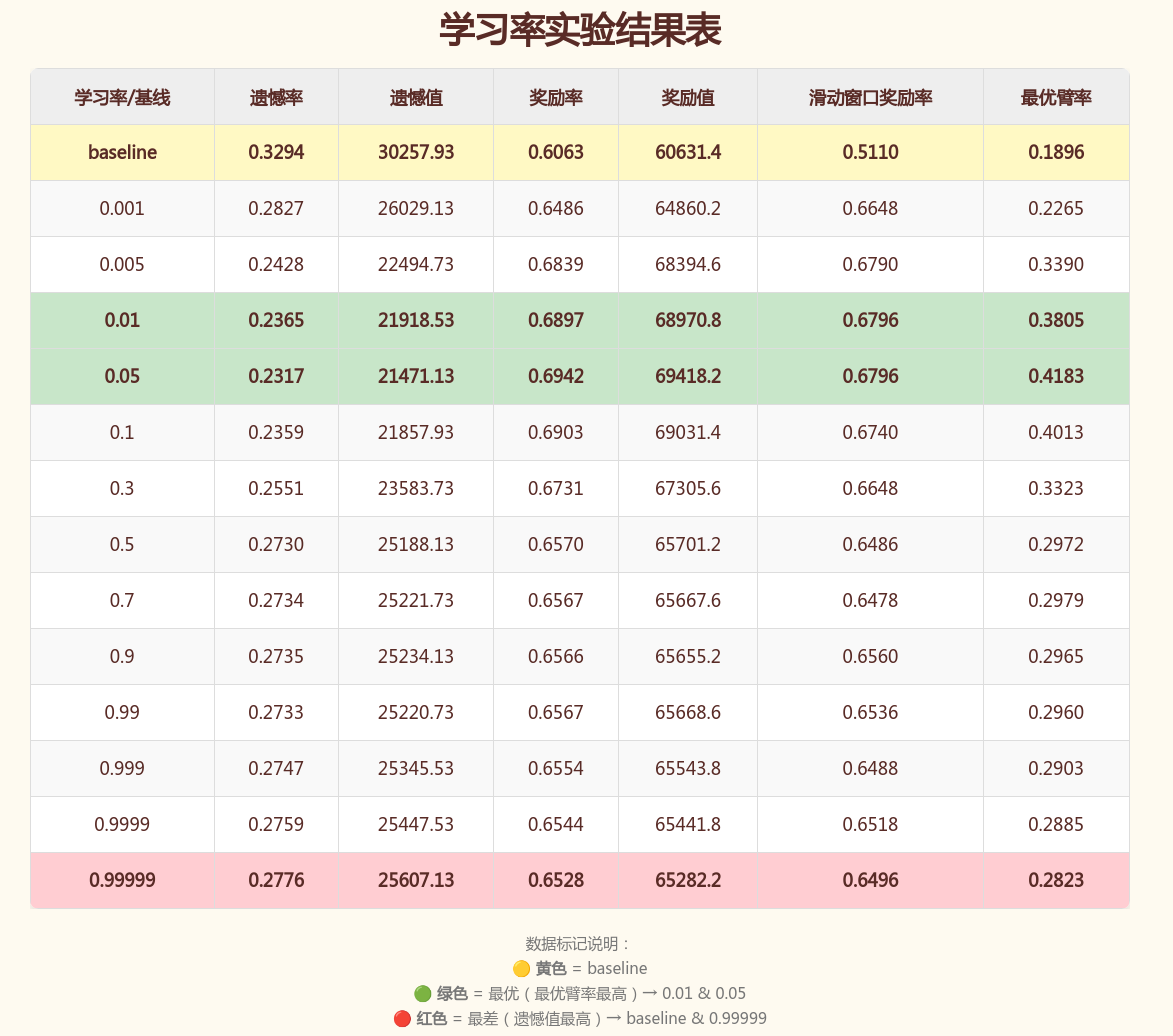
• 指标统计可信度表(95% CI)

单独图表

• 基线：

  

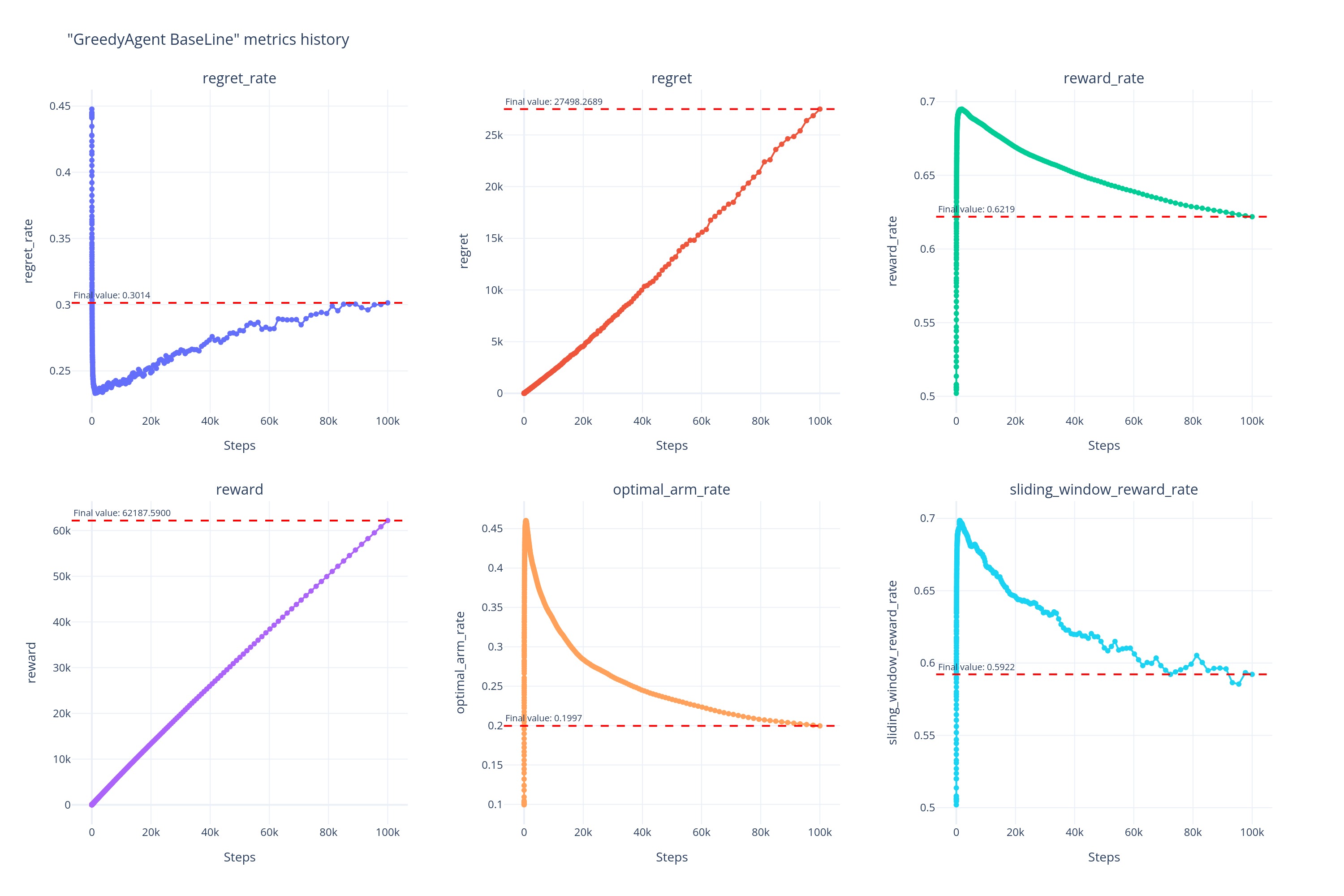
• 各学习率下 ​Greedy 的表现

  学习率	算法表现
  0.001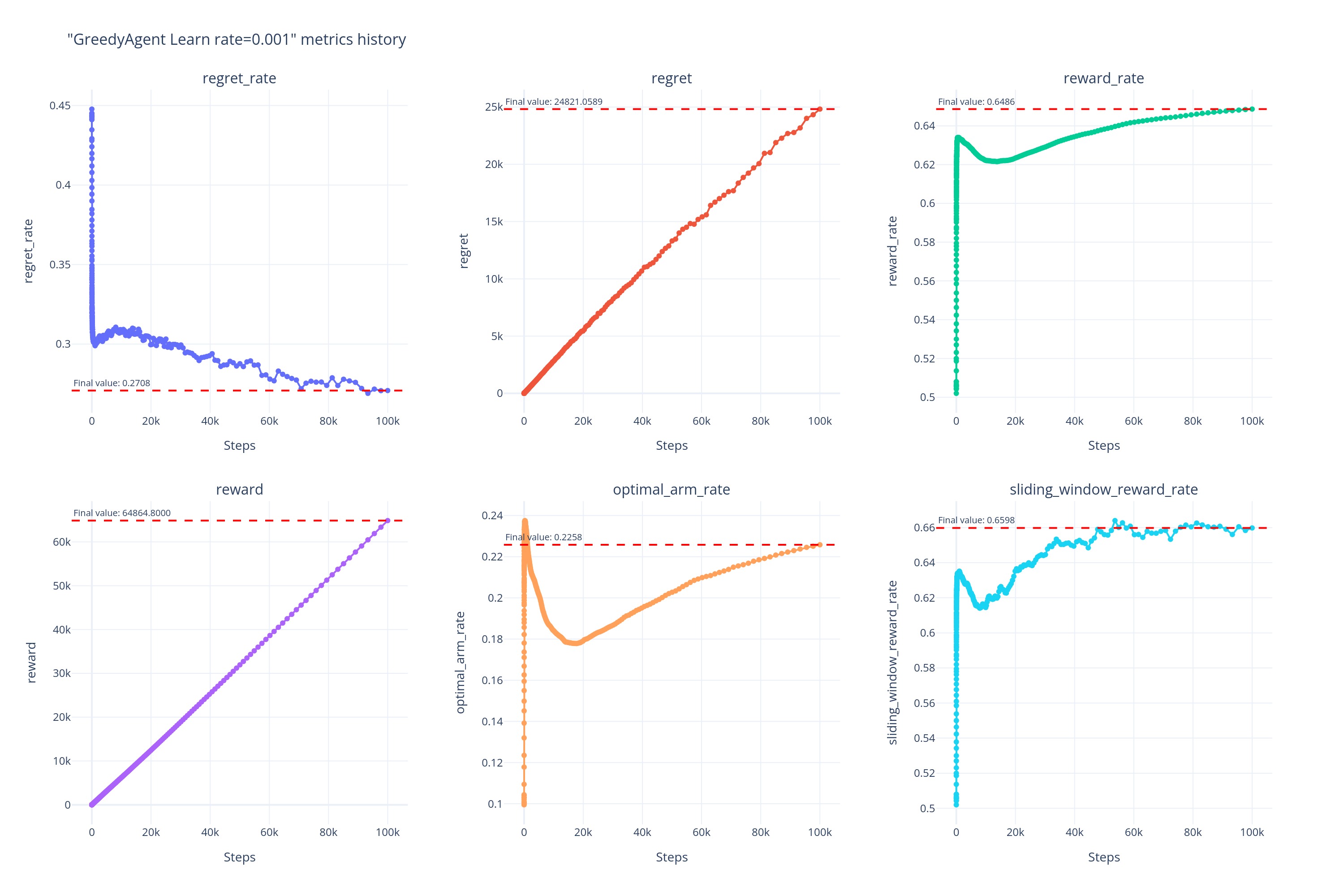
  0.005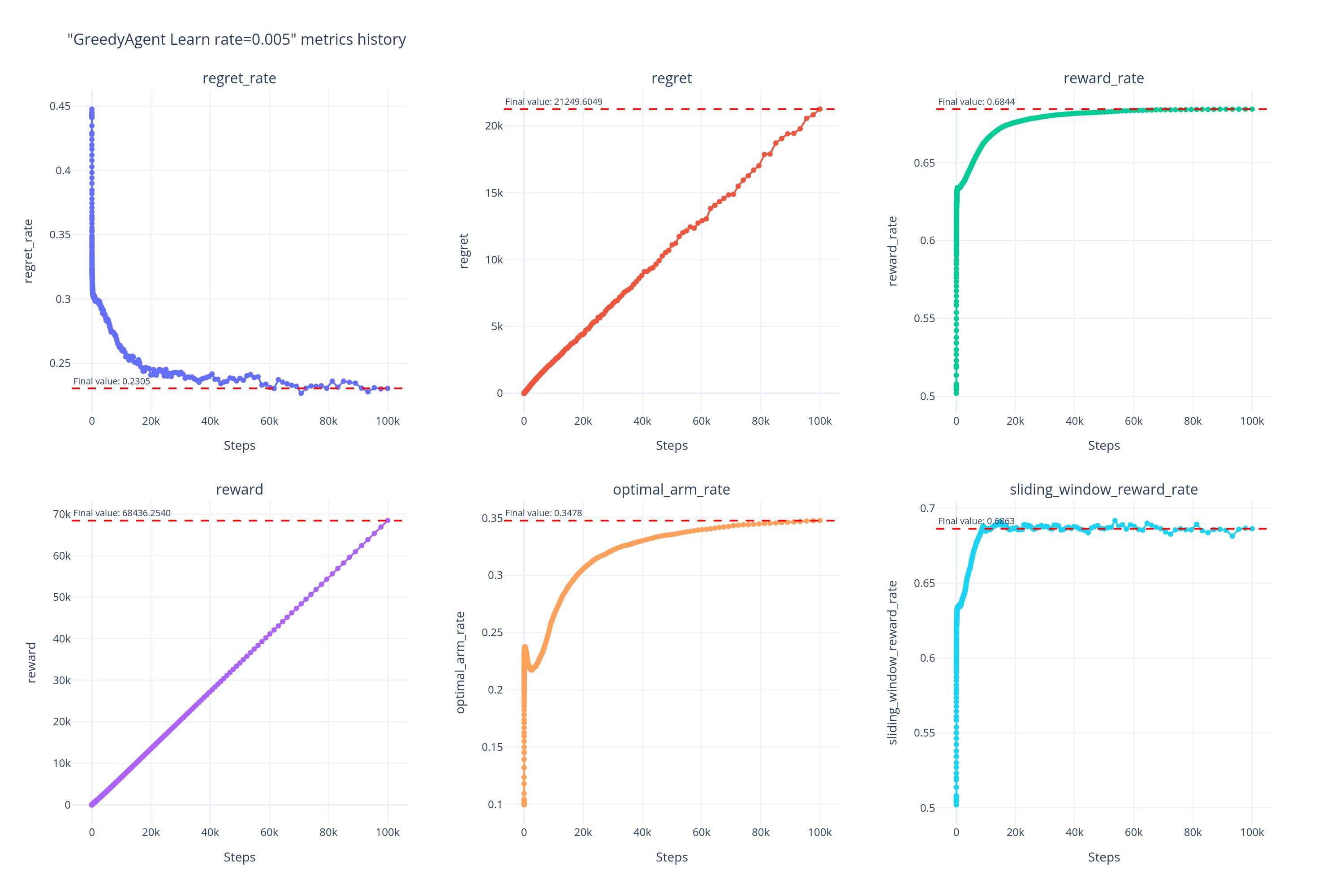
  0.01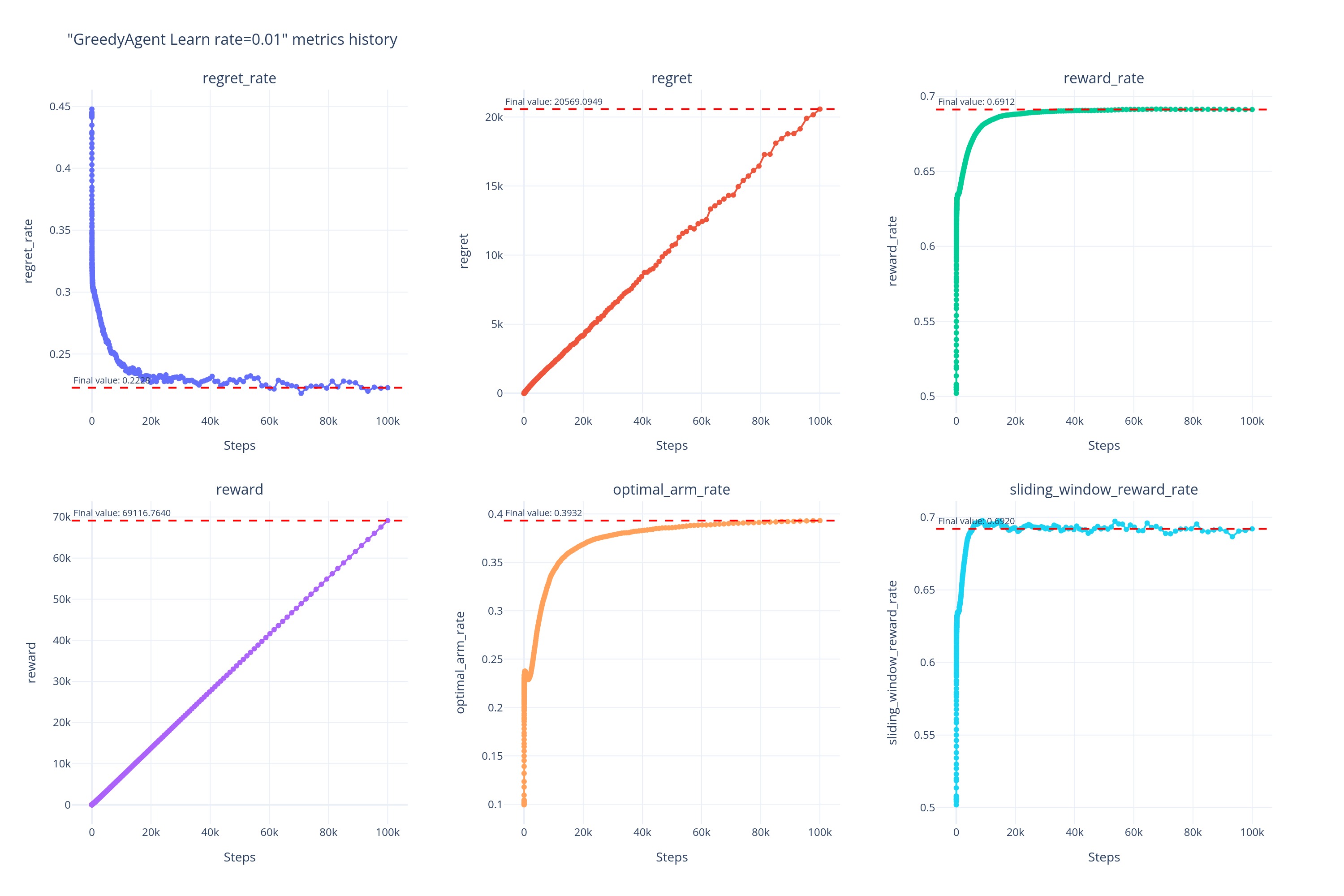
  0.05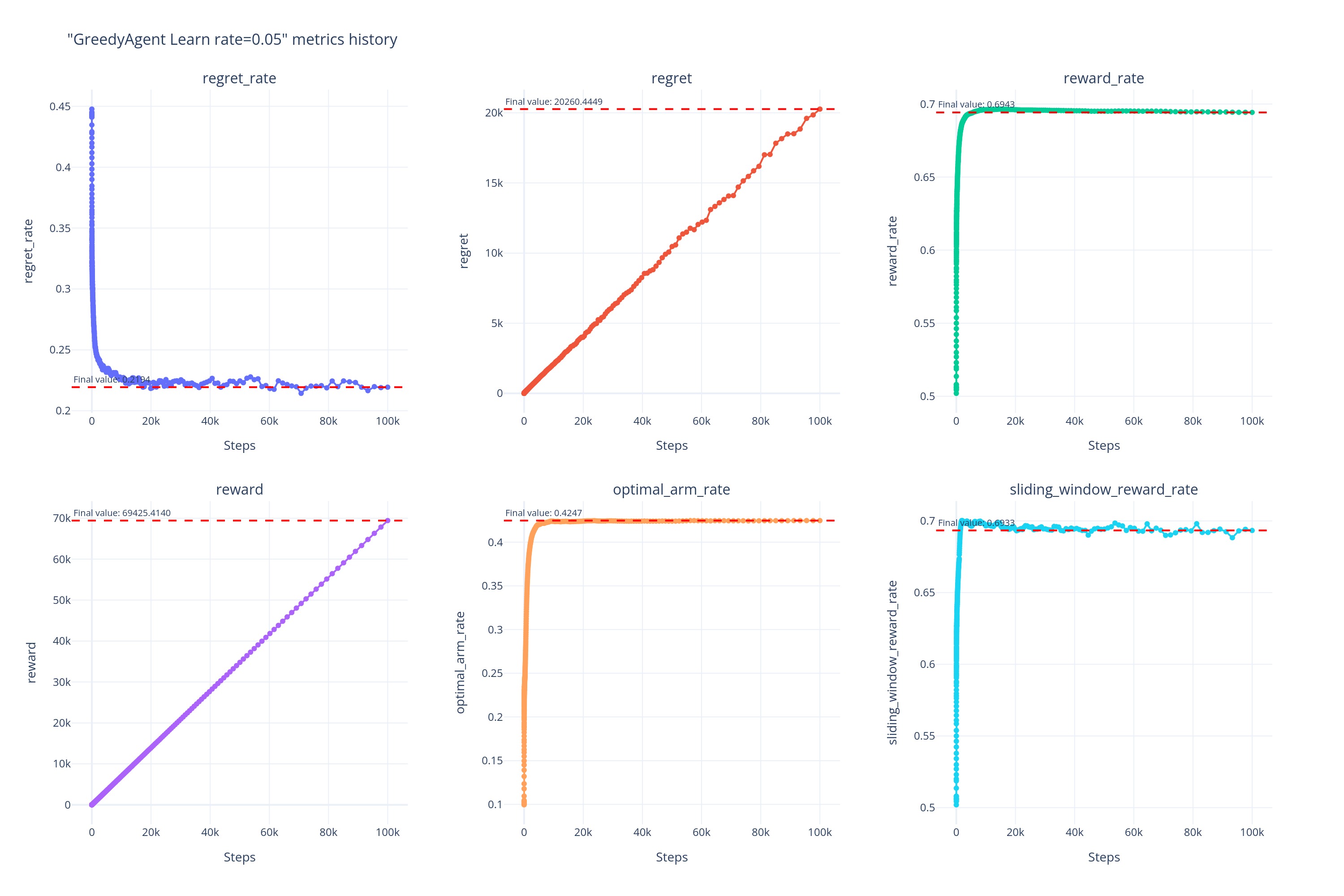
  0.1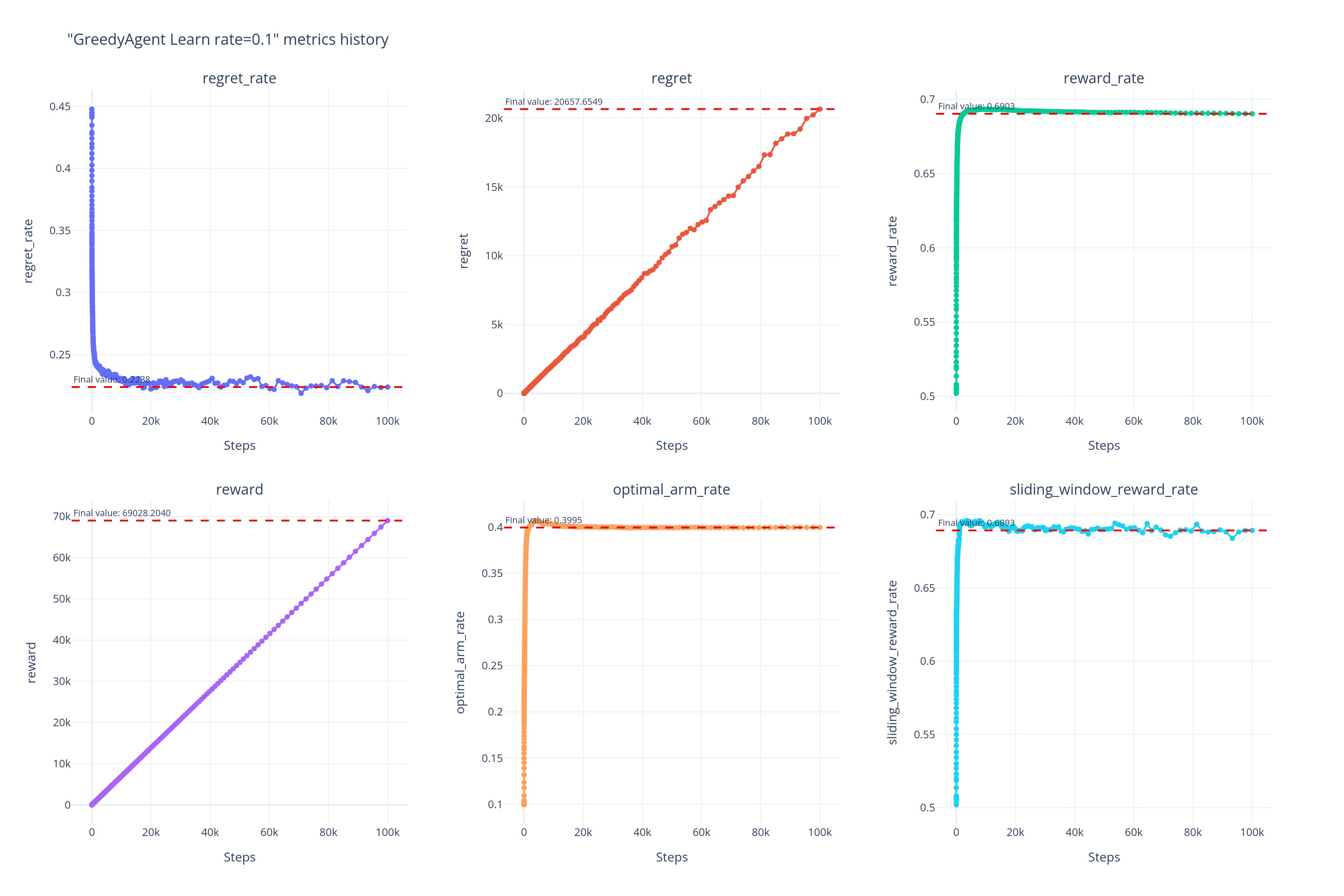
  0.3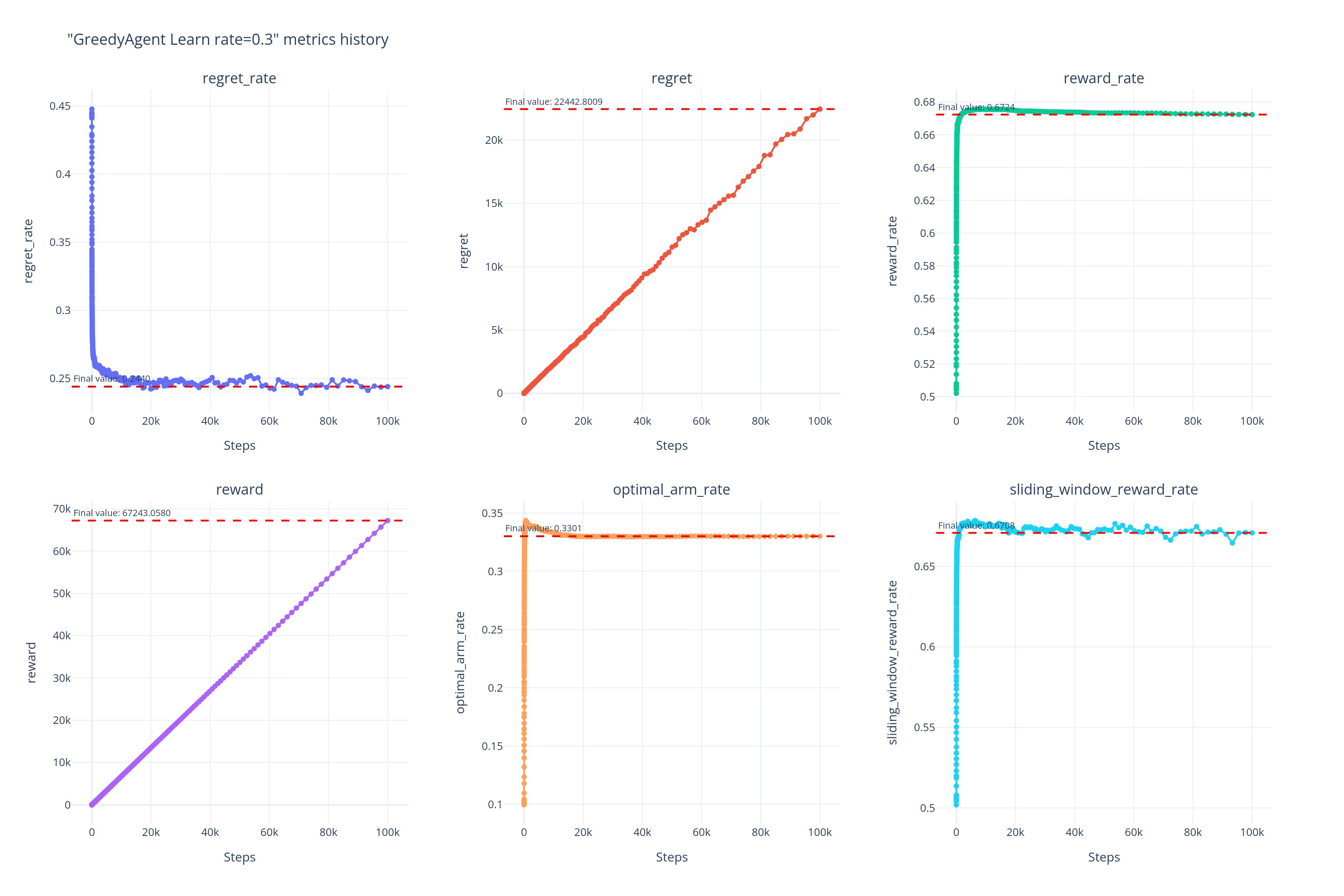
  0.5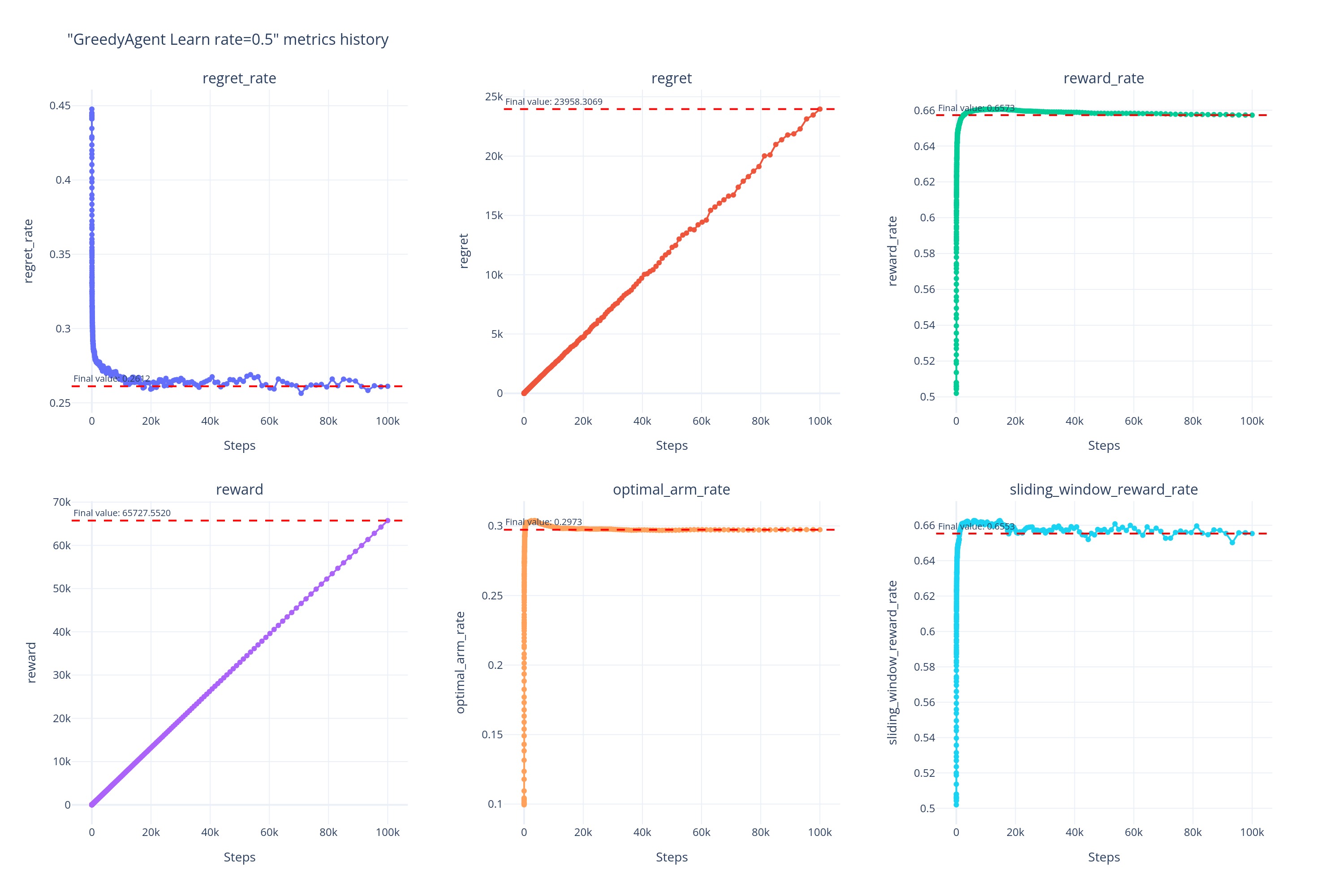
  0.7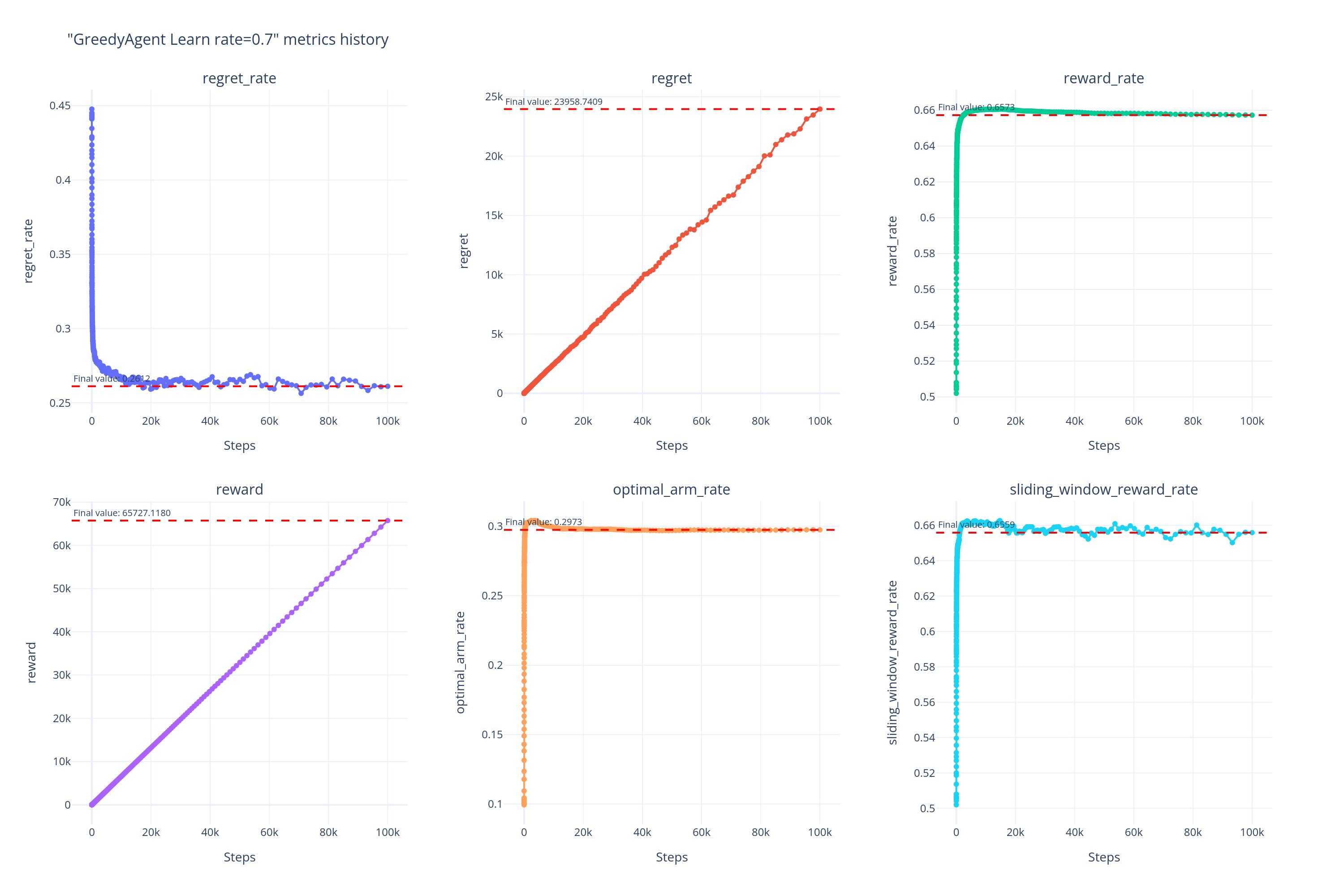
  0.9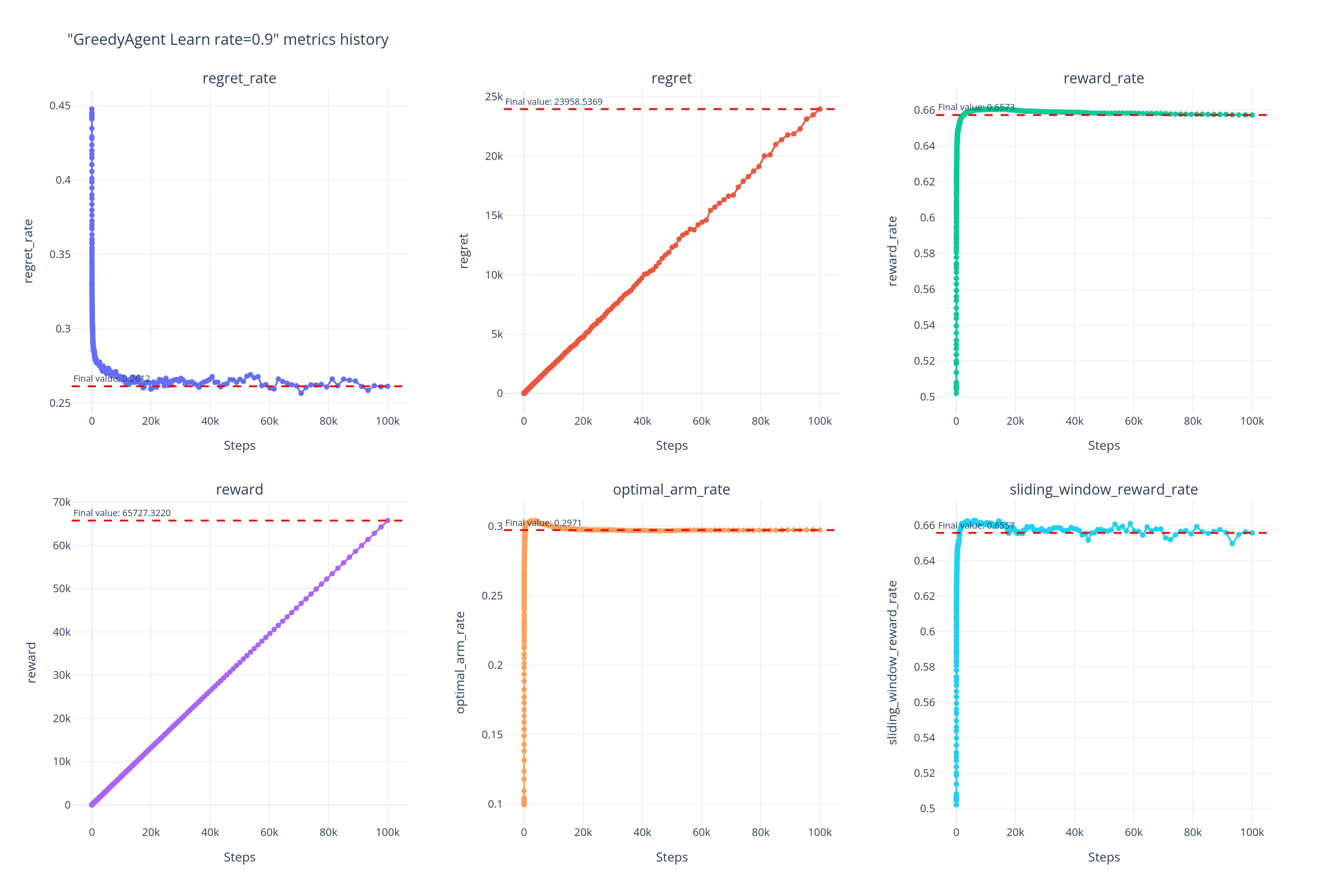
  0.99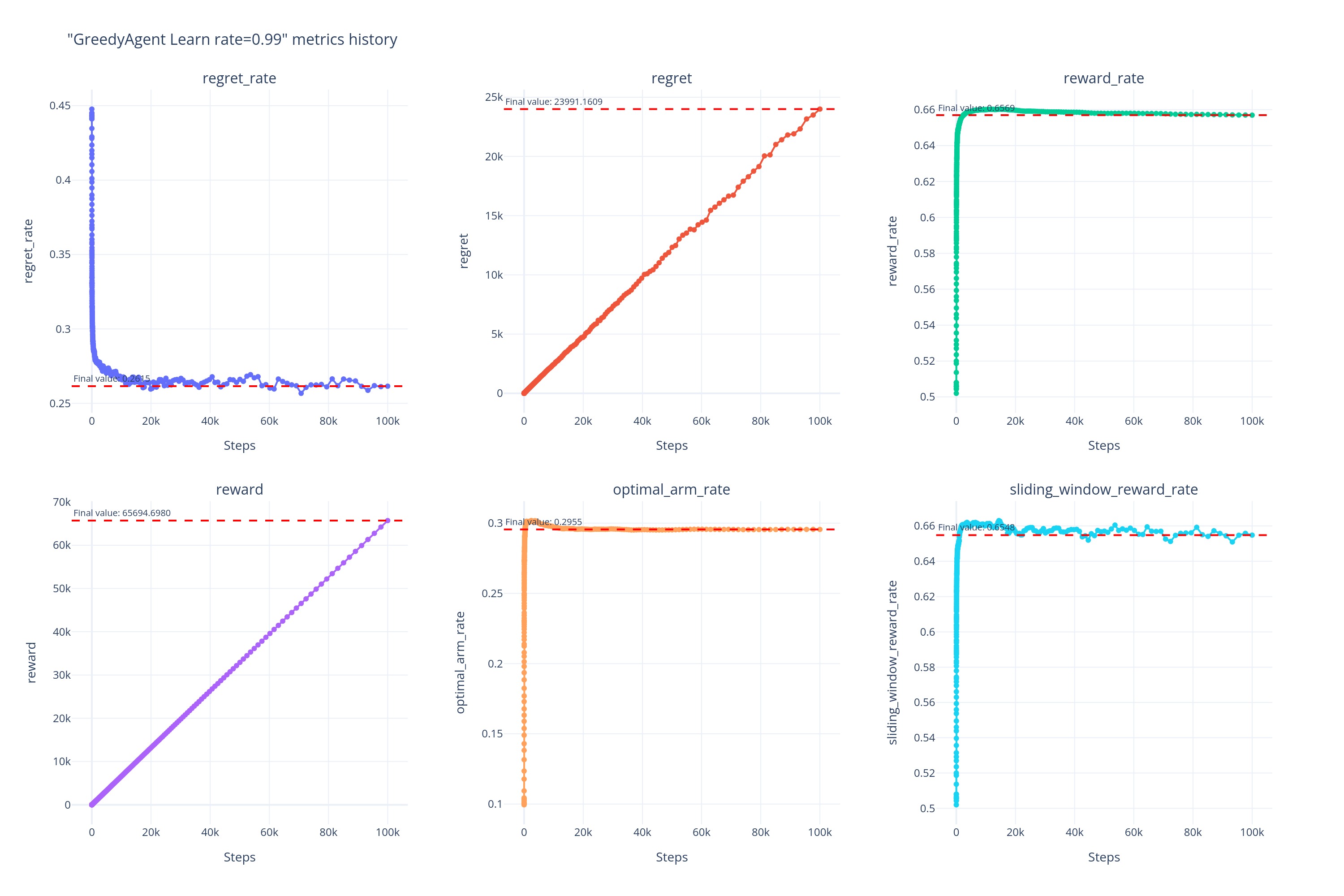
  0.999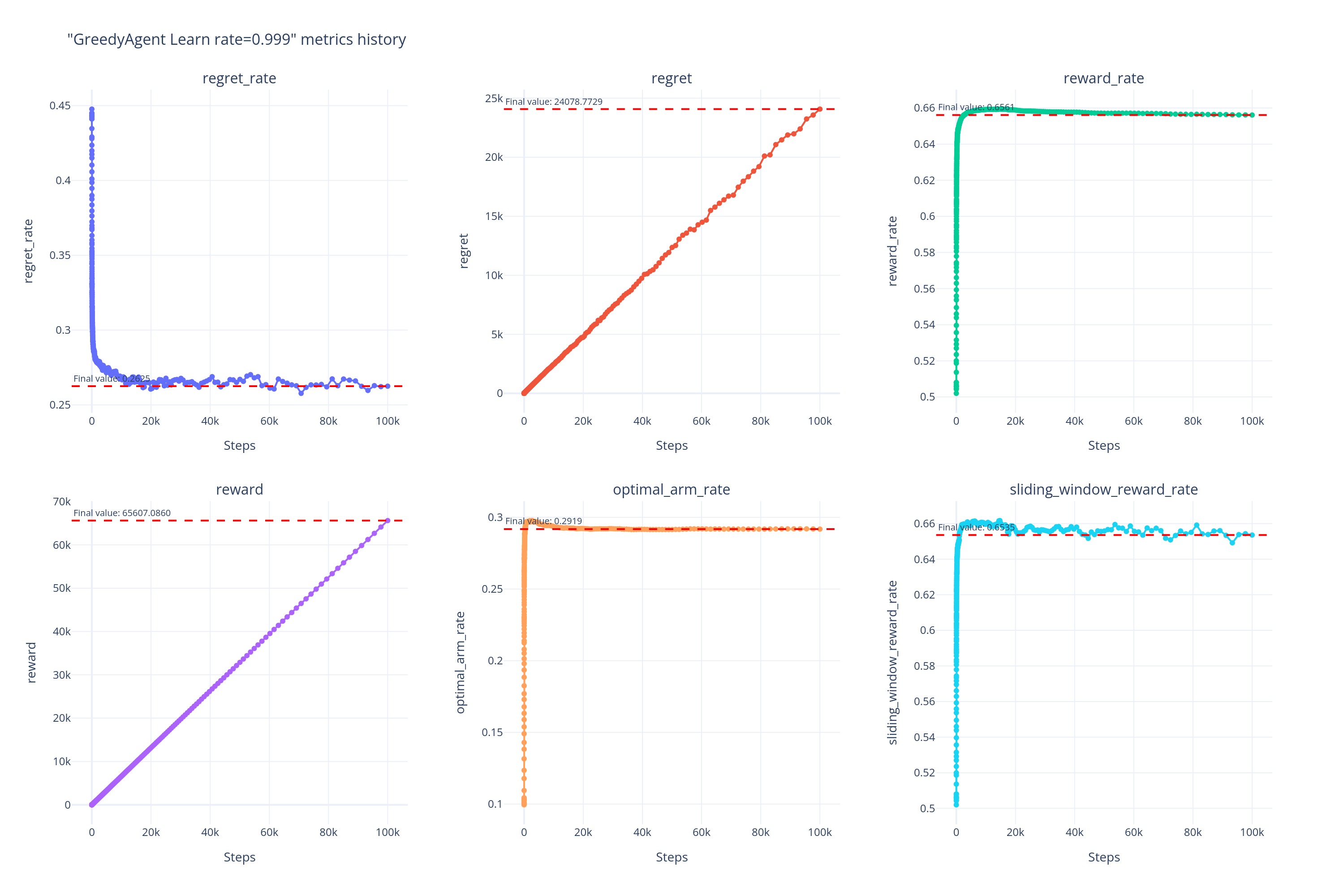
  0.9999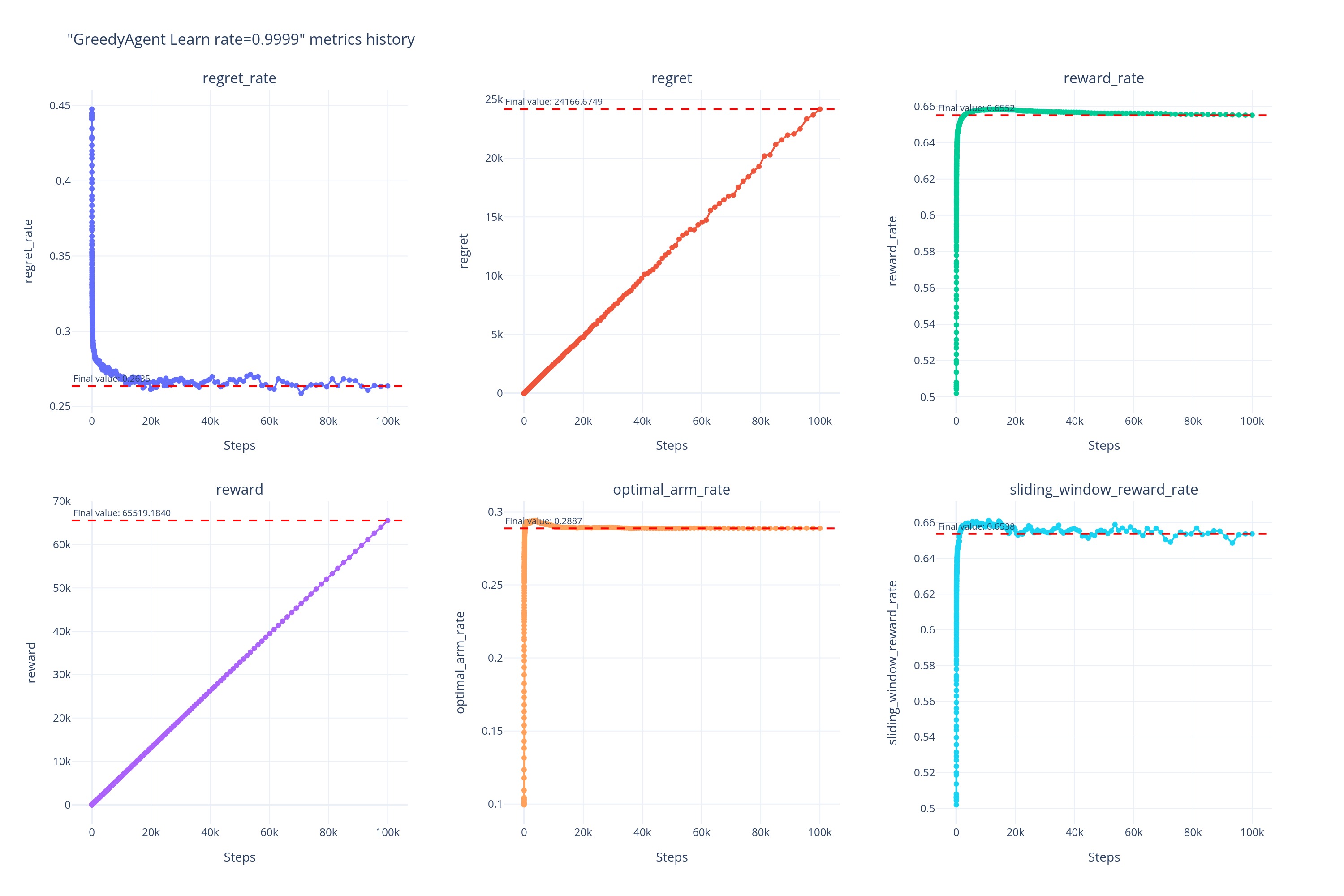
  0.99999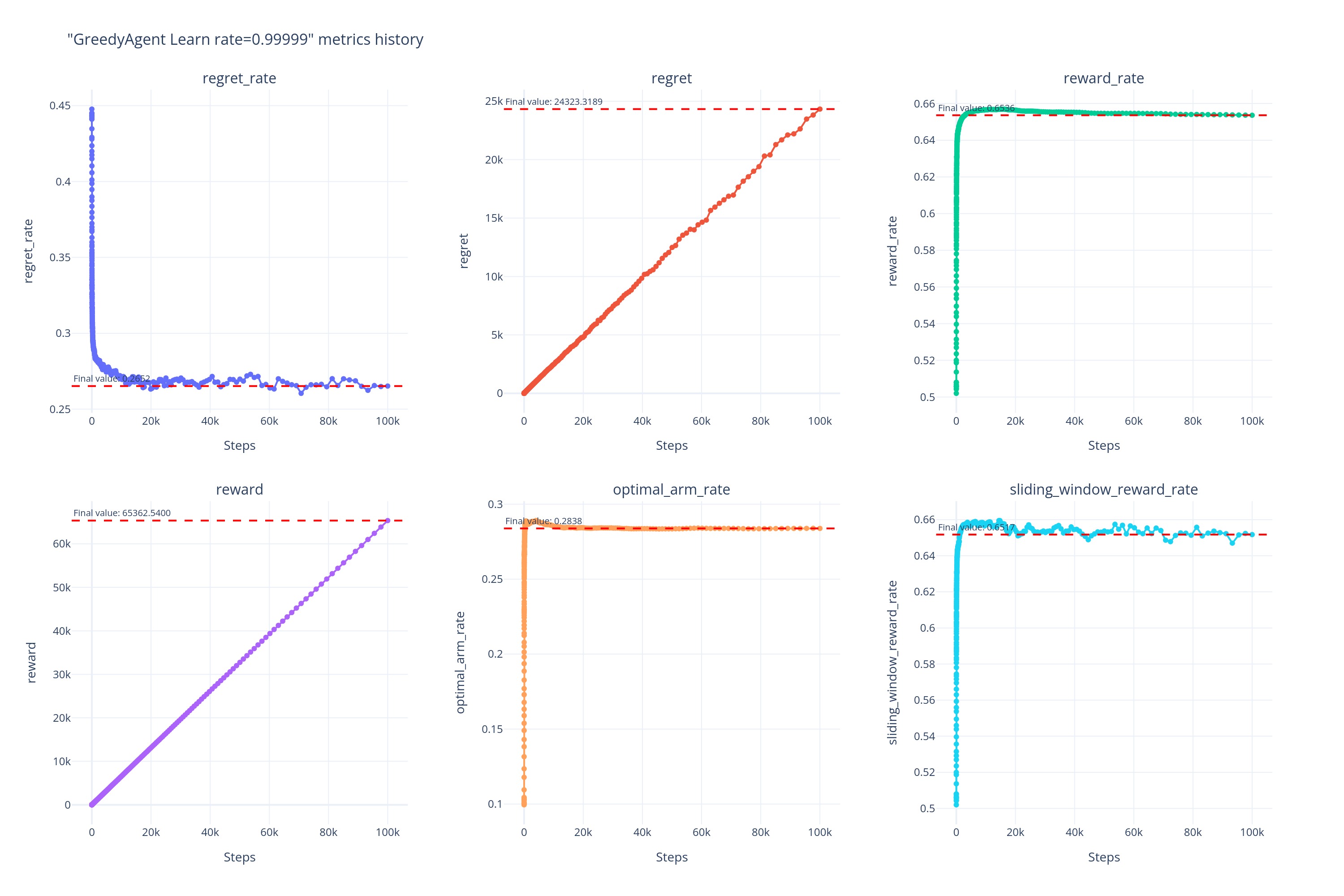

实验现象

通过对 ​Greedy 算法在 ​10^5 内不同学习率(​\alpha)下的各项指标进行观察和对比，我们发现了如下实验现象：

1. 总体性能： ​\alpha=0.05 时 ​Greedy 表现最优，Baseline 的表现差于学习率为任何值下的 ​Greedy 。

从最终的后悔率、后悔值、奖励率、奖励值、最优臂命中率和滑动窗口奖励率等多个核心指标来看，各个学习率下的 表现均优于样本均值下的 ​Greedy。

在 Baseline 下，由于在动态环境中，早期的经验往往是有效的，而过往的经验往往成为负担，因此出现了基线的各项指标在早期虽然较为领先，但是导致后期就急速下降的现象。

而对于恰当的学习率，即 ​\alpha=0.05 时，由于算法可以及时的忘掉早期已经失效的经验，并保留足够短期内有效的经验，因此虽然在早期的性能表现不如 Baseline，但是在中期便进行了反超，且性能一直保持稳定，波动并不明显。

2. 最佳臂命中率、后悔率、奖励率和滑动窗口奖励率分析

最佳臂命中率是衡量算法能否在环境变化后准确找到并持续选择最优动作的关键指标。

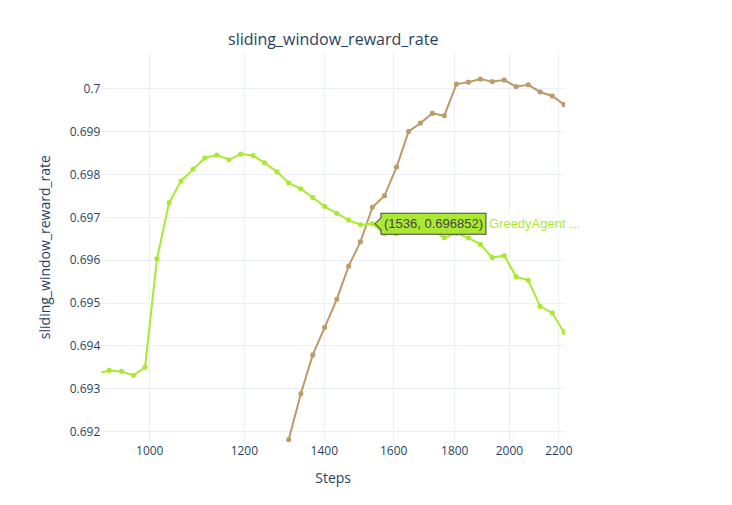
在 Baseline 下，最佳臂命中率在 ​t=611 左右时便达到了最高点，之后持续下滑；后悔率在 ​t=1112 左右时便达到了最低点，后续则波动性的上涨；奖励率则是在​t=1891 左右便达到了最高点，后续持续下滑；最后是滑动窗口奖励率，在​t=1192左右时达到最高点，后续也持续下降。

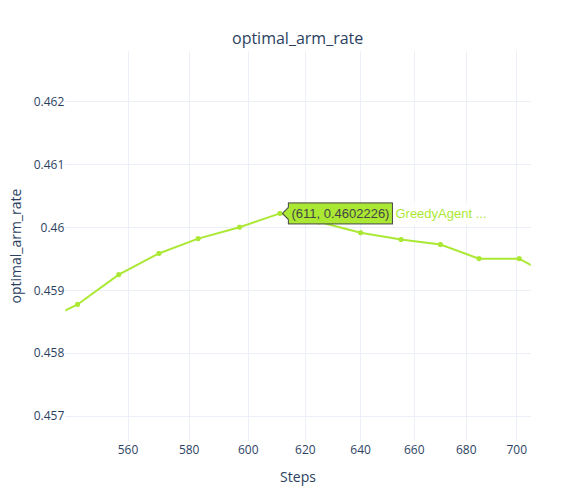
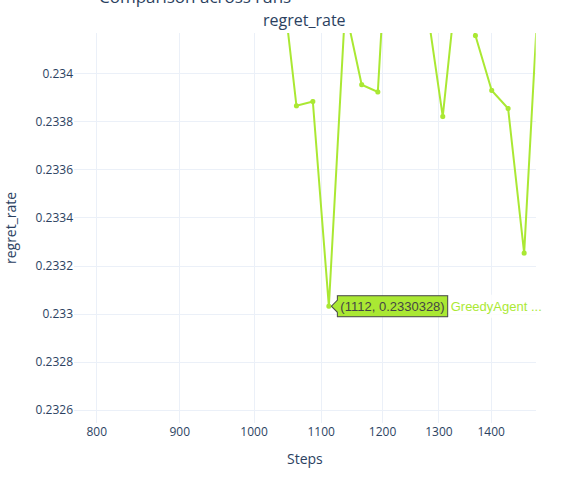
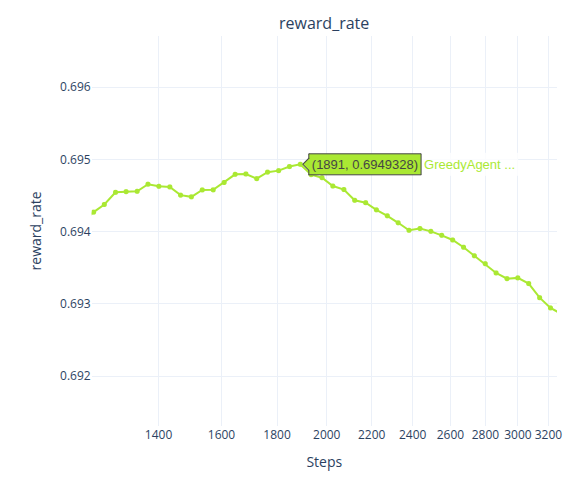
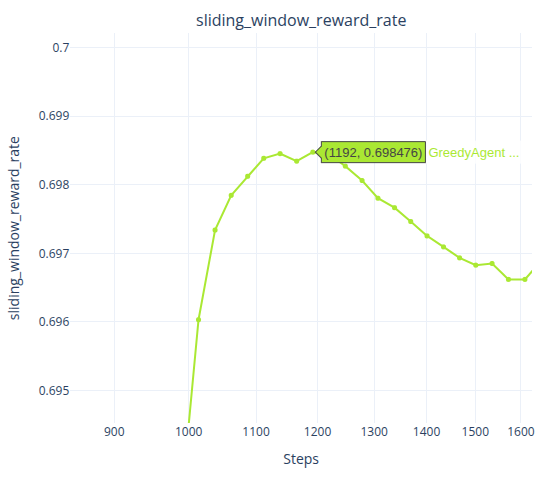
对于 ​\alpha=0.05 的 ​Greedy，则是各项指标在 ​t=2000 左右时，便达到了最高点，且基本不再发生大的波动，一直保持一个比较平稳的曲线。

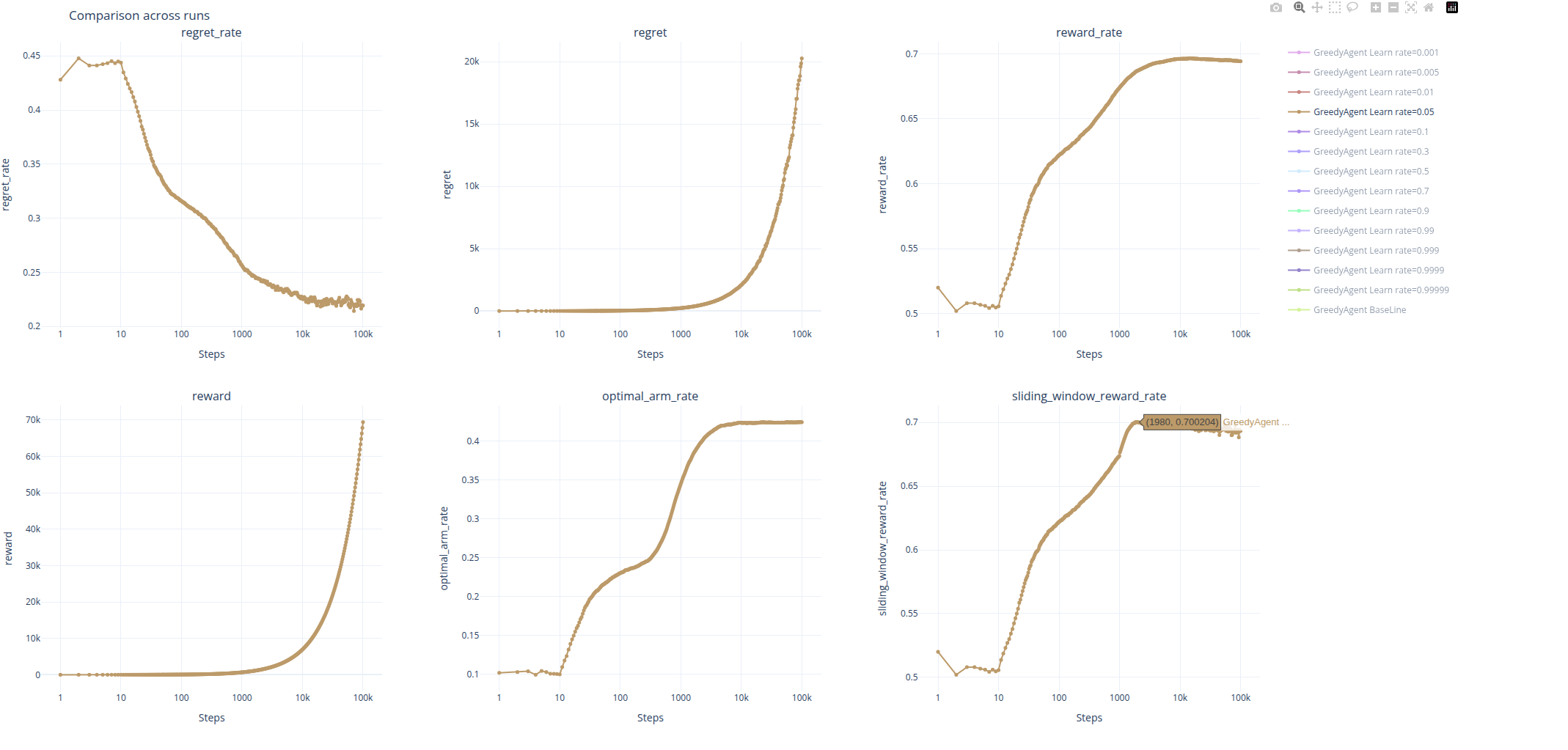
而当 ​\alpha \neq0.05 时，不论学习率是上调还是下调，可以看出性能都会下降，因此可以认为当前的动态环境中，​\alpha^*\approx0.05。

当 ​\alpha\ll0.05，如当 ​\alpha\le0.005 时，Agent 的学习速度过慢，导致在前中期的表现反而一直不如 Baseline，在后期才逐渐超越。

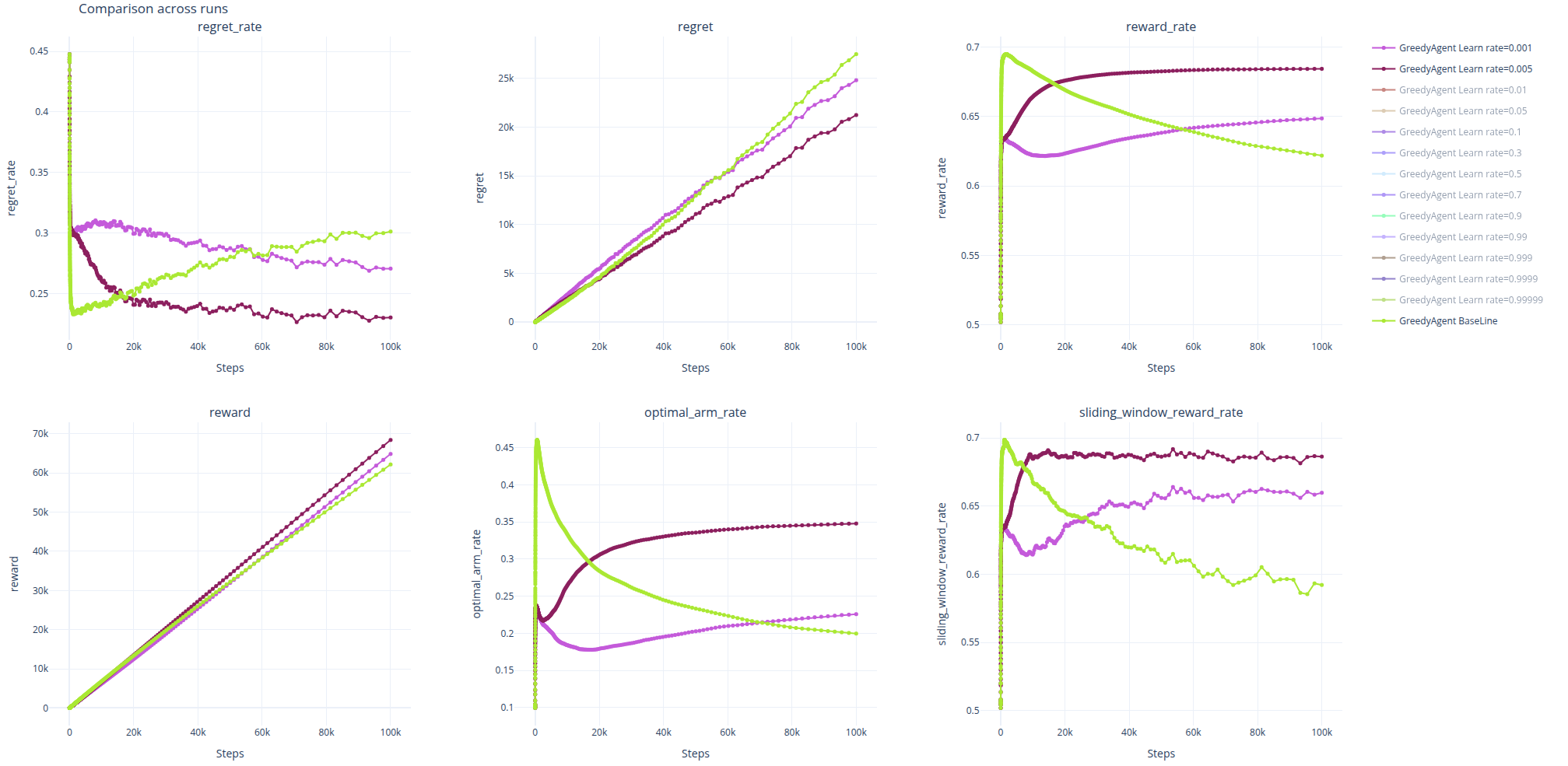
而当​\alpha\gg0.05时，如当 ​\alpha\ge0.5时，虽然 Agent 避免了因记住早期过时经验导致的受到过去经验的制约，但也因为记忆过短导致无法记住近期的有用信息，所以可以看到​\alpha\ge0.5时的曲线几乎重合在一起，并且早早的便陷入了相对来说更次的次优解。

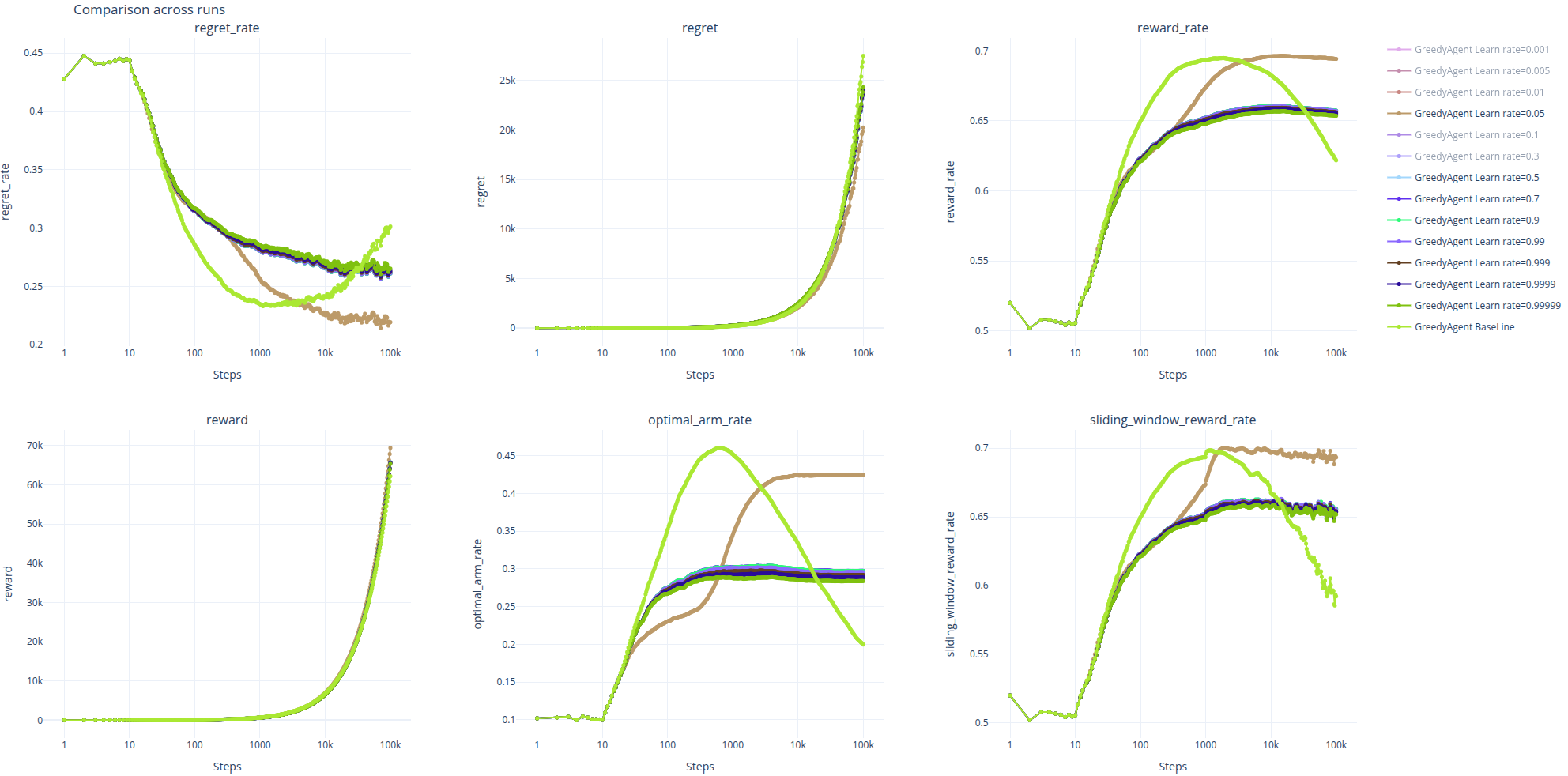
3. 统计可信度分析

   针对我们统计可信度的表格，我们可以发现。

   当 ​\alpha=0.005 的时候，统计置信区间最窄。

   而对于 BaseLine，则统计置信区间最宽。

   不过从图中我们可以看到，不论即使是最宽的情况下，其实也并没有多宽：

   

   可见 ​Greedy 的稳定性本身就是非常稳定的。

4. 总体分析

总的来说，在样本均值的 Q 值更新方法下，​Greedy 在 ​t\in(500, 1500)时，可以保持一定的优势，但在 ​t>1500 后，Baseline 的表现便被学习率为 0.05 时的 ​Greedy 所反超。

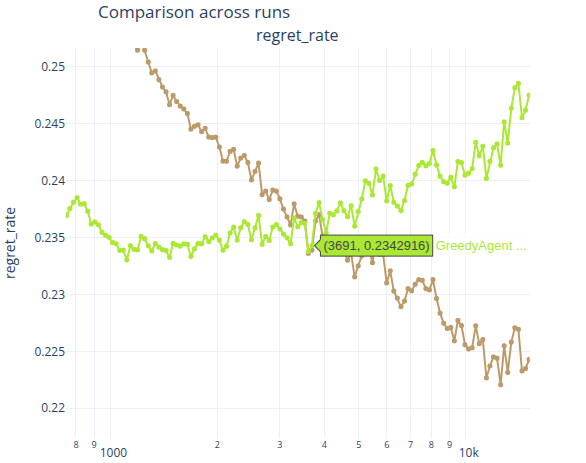
以及，当学习率在一定程度内时， Agent 可以因遗忘了早期失效的经验而不受到早期失效经验的影响的同时，保留近期有效的经验，进而达到在动态环境中保持性能稳定的效果。如果学习率设置的太小，Agent 会因为无法及时的忘掉过去的经验导致性能提升速度极慢；但如果设置的太高，又会因为近期保留的经验过少而无法进一步的提升性能。

实验结论

本次实验系统性的比较了贪婪算法的 Q 值在不同的更新方法下，在动态多臂老虎机上的性能。实验结论如下：

1. 核心结论：常数步长更新比样本均值更新更合适在动态环境中使用。在常数步长值合适时，它可以在“遗忘”与“学习”中取得在前中期以后最高的效率。 样本均值更新因无法遗忘过时的经验而被过时经验在前中期后严重拖累性能，常数步长更新所设置的值过低会因为遗忘速度过慢而遇到和样本均值更新类似的问题——被过时经验严重拖累性能；所设置的值过高又会因为遗忘速度过快，无法记住近期有效的经验而无法进一步提升性能；只有当常数步长值合适时，才能取得在“遗忘”和“学习”中最佳的效率。

2. 更新方式的策略分析：

   • 样本均值更新：该更新方式将认为所有的的经验都是同等重要的，其更新方式是取所有经验的均值来决定一个臂的 Q 值，这在动态环境中无法遗忘过时经验，进而导致性能下降
   • 常数步长更新：该更新方式可以在“遗忘”和“学习”间进行手动设置来决定平衡，这可以在动态环境中遗忘过时经验，来保证性能的平稳。

3. 总结和启示： 该实验结果表明，在动态多臂老虎机问题中，算法的 Q 值更新方法对“遗忘”和“学习”的取舍是决定其性能的关键。**​\alpha\approx0.05**时的常数步长更新方法，能够在当前的动态环境中很好的平衡“遗忘”和“学习”两种机制，从而在整体性能上超越样本均值更新与​\alpha\gg0.05或​\alpha\ll0.05时的常数步长更新方法。

附录

实验 notebook

实验仓库