不同乐观初始化次数下的各贪婪算法的性能对比

实验条件

• 环境：50 臂伯努利分布多臂老虎机，每臂真实均值均平均分布于 (0,1)

• 步数：每次实验 10,000 步。

• 运行次数：50 次独立实验。

• 算法：

  • 普通贪婪算法（Greedy）
  • 固定 ​\epsilon-greedy
  • 退火 ​\epsilon - greedy

• 变量：乐观初始化值​Q_0 \in[1, 5, 10, 15, 30, 50, 100]

实验目的

验证乐观初始化大小对三类贪婪策略表现的影响。具体关注：

• 总奖励 (avg_total_reward)
• 累积 regret (avg_regret, avg_regret_rate)
• 最优臂命中率 (avg_optimal_rate)
• 收敛速度 (avg_convergence_steps)

实验结果

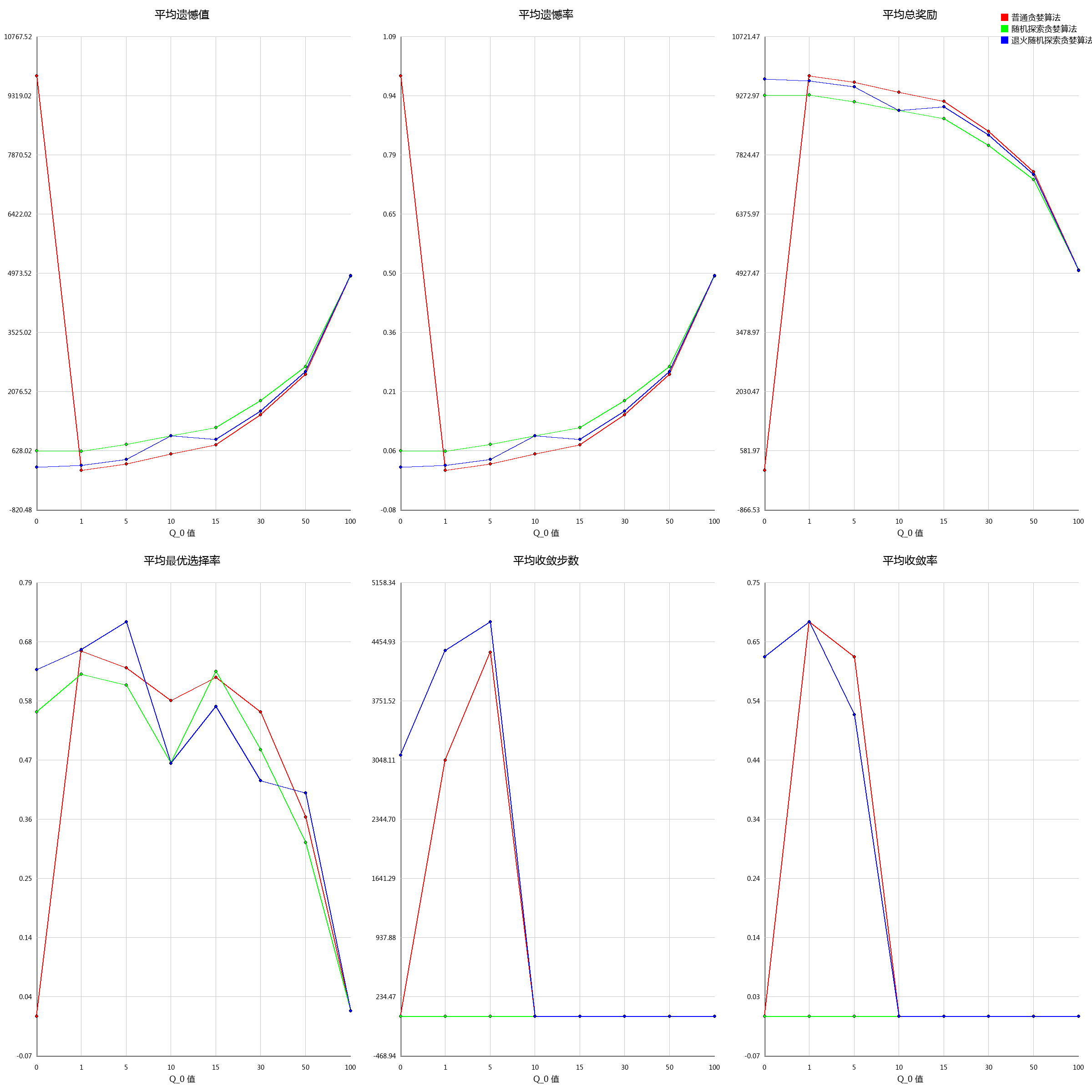
实验结论

在 ​Q_0 = 0 的时候，各算法中退火随机探索贪婪算法表现最好。

但在​Q_0 = 1的时候，普通贪婪算法表现最好，且各指标略优于退火随机探索贪婪算法。

但是在 ​Q_0 值持续上升的时候，负面指标（平均遗憾率，平均遗憾值，平均收敛步数）均上升，直到​Q_0=30 的时候，模型已经无法收敛。

而对于正面指标（平均总奖励，平均最优臂选择率，平均收敛率）除了平均最优臂选择率略有波动以外，其他指标与初始Q值设定呈负相关关系，即：初始Q值越高，算法性能越差。

因此我们可以得到这样的一个结论：

对于当前的场景下，奖励符合伯努利分布，奖励在环境中均匀分布时，算法表现当​Q_0 = 1时最优，随后随着​Q_0的上升而下降(​Q_0 \in(1,\infin))。

你可以在这里找到我的学习过程的代码仓库。